题目大意：a的b次幂，其所有约数的和是多少？输出模9901的结果。

Description

Input

Output

Sample Input

2 3

Sample Output

15

Hint

解题思路

整数的唯一分解定理：整数a进行质因数分解，其表示方法是唯一的，a = p1^k1 * p2^k2 * … * pn^kn，其中p是质因数，k是对应质因子的次幂。

约数个数：(k1+1) * (k2+1) *… * (kn+1)，因为约数的因子，只能从质因子里面选，要么不选（选0个），要么选1到k个，每个质因子都是如此。

约数和：(1+p1+p1^2+…+p1^k1) * (1+p2+p2^2+…+p2^k2) * … * (1+pn+pn^2+…+pn^kn)，展开后，每一项代表了各个因子选的次幂，使得包含所有约数，且每个约数恰好出现1次！

题目实际上就是求这些等比数列的乘积！首先对a进行质因数分解，记录其质因子和次幂，然后次幂全都要乘以b，因为a^b，有b个a相乘。

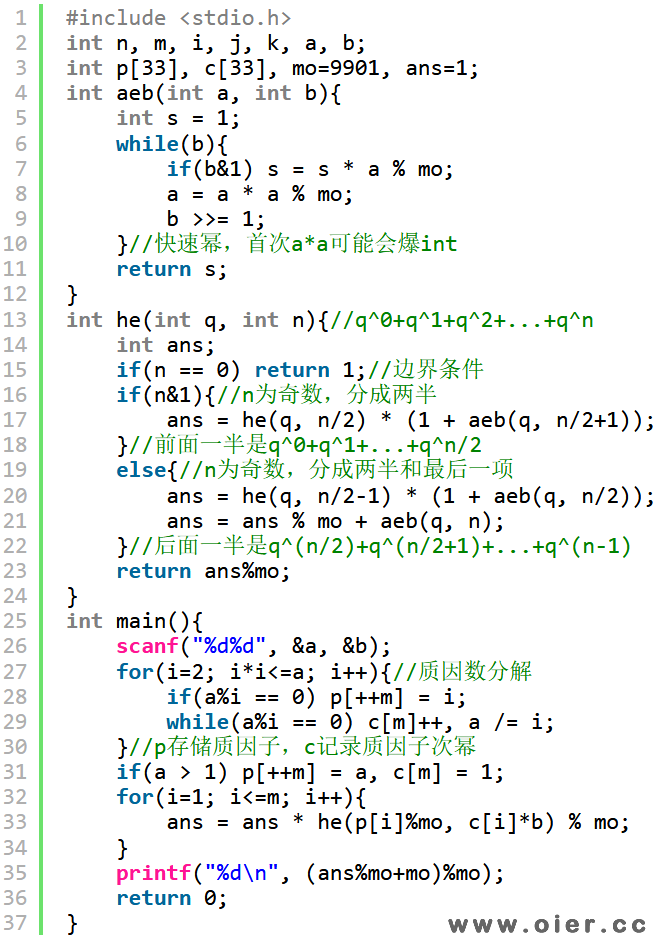
程序实现

解法一：利用等比数列求和公式，首先为1，公比为p，末项为p^n，和为( p^(n+1)-1 ) / (p – 1)，除以p-1，相当于乘以p-1的逆元（模9901）。

因为模数很小，有可能出现质数p-1是模数的倍数，不存在逆元，这种情况要特殊考虑：当p-1是9901的倍数时，p%9901 = 1，1 + p + p*p + … + p^n = 1 + p%mo + (p%mo)*(p%mo) + … + (p%mo)^n = 1 + 1 + … + 1 = n+1。

另外，需要注意快速幂中，a = a * a % mo，第一次a有可能很大，a*a会爆int，应先取模后再相乘，或者改用long long类型。

根据欧拉定理，可以用快速幂求逆元：若gcd(p, mo) = 1，那么p^(Φmo) % mo = 1；因为9901是质数，所以p的逆元就是p^(mo-2)。

如果不会求逆元，还能用分治的方法来求等比数列的和：

当n是奇数时：1+p+p*p+…+p^n = (1+p+p*p+…+p^(n/2)) * (1 + p^(n/2+1))，展开后就可以得到1+p+p*p+…+p^(n/2) + p^(n/2+1) + … + p^(n)，因为n是奇数，所以p^(n/2+n/2+1) = p^n。

当n是偶数时：1+p+p*p+…+p^n = (1+p+p*p+…+p^(n/2-1)) * (1 + p^(n/2)) + p^n，展开后就可以得到1+p+p*p+…+p^(n/2) + p^(n/2+1) + … + p^(n)。