题目大意：3个格子填入3个数，需要满足一定要求，这三个数的和最大是多少？

描述

如上图，有3个方格，每个方格里面都有一个整数a1，a2，a3。已知0 <= a1, a2, a3 <= n，而且a1 + a2是2的倍数，a2 + a3是3的倍数， a1 + a2 + a3是5的倍数。你的任务是找到一组a1，a2，a3，使得a1 + a2 + a3最大。

输入

一行，包含一个整数n (0 <= n <= 100)。

输出

一个整数，即a1 + a2 + a3的最大值。

样例输入

3

样例输出

5

解题思路

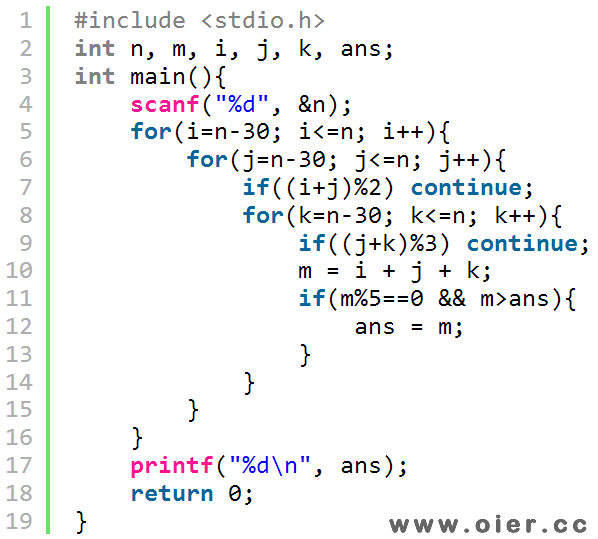
分别枚举第一个格子、第二个格子和第三个格子里面的数字，判断是否满足条件，如果满足条件，则计算他们的和，如果更大，更新最大值。

如果数据不是100，而是1000，甚至10000，或者多组测试数据，如何优化？

1、在枚举下一个数之前，先判断当前是否符合要求，符合才继续枚举（类似于搜索的可行性剪枝）

2、先找到第一个满足要求的数，然后如果是3的倍数，那么之后每次家加3……

3、不难发现，如果找到3个满足要求的数字后，任何一个数字加上30，还是满足条件的，所以只需要枚举n-30到n，而不需要枚举1到n。

程序实现