LOJ149-01分数规划
2513+
题目大意:n个物品,价值是a,价格是b,选出m个,性价比最高是多少?
n个物品,第i个物品价值是ai,费用是bi,购买m个,性价比(∑ai/∑bi)最大是多少?
解题思路
二分猜答案,假设最佳答案是M,我们猜的是m,那么对于选了的物品,M=∑ai/∑bi,如果猜的m小了,那么M >= m,即∑ai/∑bi>=m,也就是\sum{a_i} – m * \sum{b_i} >= 0,在已知“答案”的情况下,我们可以直接贪心选择a_i – m*b_i最大的物品,如果选k个后非负,那么答案猜小了,或许可以更大;如果是负数,那么猜大了,答案要更小一点。
程序实现

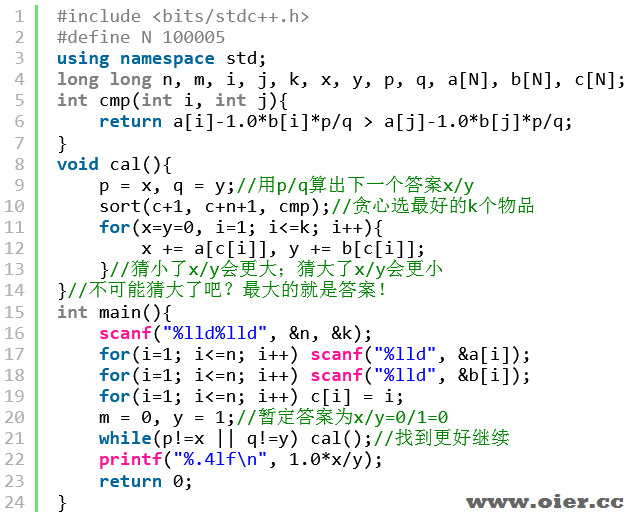
Dinkelbach算法:迭代猜答案。从最小的答案x=0/y=1开始猜,如果猜小了,那么\sum{a_i} / \sum{b_i} > x/y,我们继续猜\sum{a_i} / \sum{b_i},这样能比较快的猜出答案,猜不到更大的就停止循环。