题目大意：学生的成绩经常会变，老师们很喜欢询问，从x号到y号当中，分数最高的是多少，如何快速回答？

Problem Description

很多学校流行一种比较的习惯。老师们很喜欢询问，从某某到某某当中，分数最高的是多少。

这让很多学生很反感。

不管你喜不喜欢，现在需要你做的是，就是按照老师的要求，写一个程序，模拟老师的询问。当然，老师有时候需要更新某位同学的成绩。

Input

本题目包含多组测试，请处理到文件结束。

在每个测试的第一行，有两个正整数 N 和 M ( 0<N<=200000,0<M<5000 )，分别代表学生的数目和操作的数目。

学生ID编号分别从1编到N。

第二行包含N个整数，代表这N个学生的初始成绩，其中第i个数代表ID为i的学生的成绩。

接下来有M行。每一行有一个字符 C (只取’Q’或’U’) ，和两个正整数A，B。

当C为’Q’的时候，表示这是一条询问操作，它询问ID从A到B(包括A,B)的学生当中，成绩最高的是多少。

当C为’U’的时候，表示这是一条更新操作，要求把ID为A的学生的成绩更改为B。

Output

对于每一次询问操作，在一行里面输出最高成绩。

Sample Input

5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5

Sample Output

5
6
5
9

解题思路

如下图，把1到n个学生看成一条[1,n]的线段，如果线段长度超过1，不断地分成2半，直到长度为1。题目要求回答区间最大值，那么我们每一条线段就记录该区间的最大值。

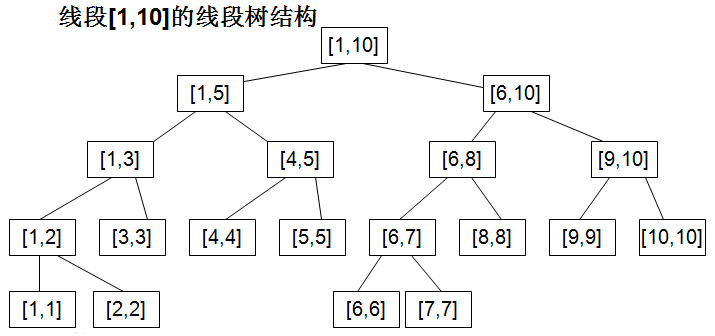
首先是单点修改：修改的时候，我们可以递归找到对应的长度为1的线段，如修改第k个学生的成绩，那么找到线段[k,k]，修改他的值即可。长度为1的值被修改了，有可能影响到包含它的线段的最大值，故在回溯的时候，即搜索完左右儿子后，需要更新父亲结点的最大值。由于每次分成两半，递归深度在log2n范围内，每次修改时间复杂度是O(log2n)。

其次是回答询问：如询问[x,y]区间的最大值，我们可以从根结点开始搜索，如果[x,y]完全包含根结点，那么我们不需要在往下找了，因为根结点下面的所有节点的最大值以及记录在根结点；如果并不是完全包含，则左边包含就往左边找左边的最大值，右边包含就往右边找右边的最大值，最终取这两个值的最大值即可。对于每次询问，时间复杂度也是O(log2n)，因为如果询问的区间很大，两边都有，那么左右两边的复杂度是一样的。现在只看左边的结点，如果左边的结点也是两边都有包含，那么右边区间可以直接返回；如果只是右边被包含，左边不需要搜索。也就是说，不会出现左右两边一起往下扩展的情况。

程序实现

堆结构存储：堆结构存储的优点是不需要记录该结点的左儿子、右儿子是谁，因为如果该结点变化是p，那么左儿子就是p*2，右儿子就是p*2+1。那么，数组开多大呢？4倍是不会出错的，为什么2被不行呢？从线段树的结构图可以看出，最后一层可能会突出几个叶子结点，层数是⌈log2n⌉+1，因此我们至少需要开1<<⌈log2n⌉+1大的数组（最后一层结点数是1<<⌈log2n⌉，所有层结点数需要再乘以2）。

结构体链表+动态开点：用结构体链表存储，只需要开2倍的数组就行，因为每个长度为1的点占一条线段，之后两两合并：n+n/2+n/4+…+1。动态开点，就是用到他的时候才给该结点分配空间：一开始根结点p是0，c记录当前分配了多少个结点，如果出现p=0即还没分配空间，此时++c的编号的结构体就分配给该结点；同样地，当需要进入儿子结点的时候，直接把记录儿子结点的编号的变量传过去就行，如果该编号为0，递归进入后会给他分配空间，由于传参数用的是引用(&p)，那么父亲结点对应的变量会自动修改。

为什么不需要记录线段的左右端点呢？因为在递归搜索的过程中，传参数的时候可以顺便计算出区间的左右端点，不记录左右端点可以节省空间。如果询问q远比区间n+1小，那么可以开更小的空间，因为每次查改，都是是一条链下去的，是log级别的，空间开到q*log2(n+1)*2就足够了。

紧凑存储：堆结构存储之所以浪费空间，是因为最后一层空了很多个出来，其实我们可以采用更紧凑的存储方式——每个区间[l,r]分别存储在数组中的l+r位置上。叶子结点的区间都是[i,i]的形式，那就存储在2，4，6，8……中间的空位恰好可以存储他们的父亲结点，如果出现区间[1,3]，会存在4产生冲突，那么我们规定非叶子结点都放在奇数上，即区间l!=r那么|1变成奇数，因此对于区间[l,r]的存放位置就是(l+r)|(l!=r)。

分块代码，复杂度更高，但实际速度最快：