题目大意:已知$n = \prod p_i^{e_i}$,$\lambda(n) = -1^{\sum{e^i}}$,求$\sum\limits_{k=1}^k \sum\limits_{i|k} \sum\limits_{j|i} \lambda(i) \lambda(j) $。
解题思路
首先,理解公式求的是什么,写个暴力程序验证一下:

然后,花一点点时间,改成$O(n\sqrt{n})$算法,主要是枚举约数的优化、17-20行的记忆化。
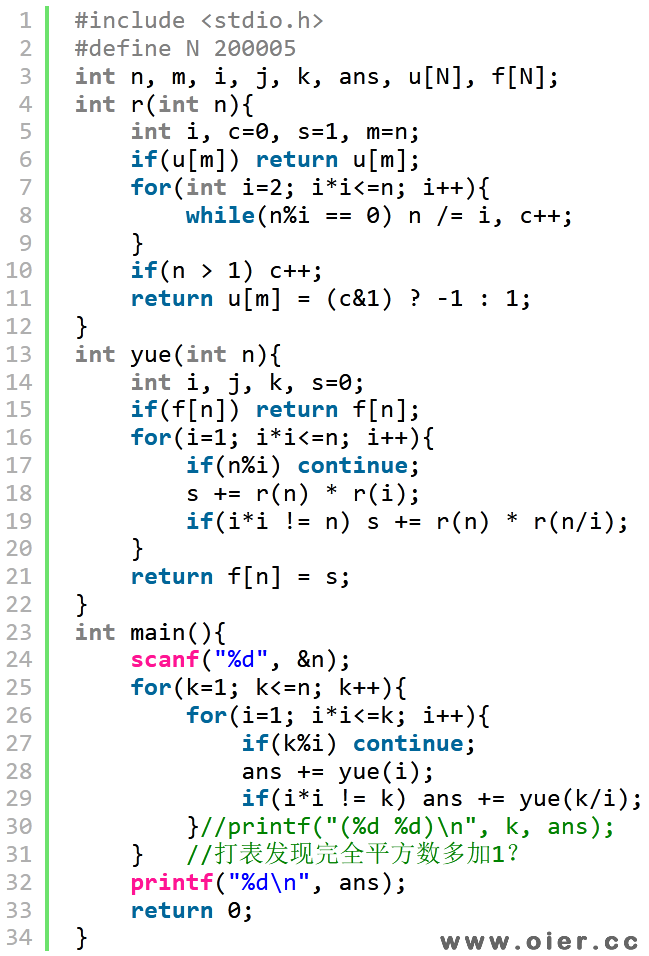
打表发现跟完全平方数有关系?推出答案是$\sum\limits_{i=1}^n \frac{n}{i^2}$。
公式推导:$\sum\limits_{k=1}^k \sum\limits_{i|k} \sum\limits_{j|i} \lambda(i) \lambda(j) = \sum\limits_{k=1}^k \sum\limits_{i|k} \lambda(i) \sum\limits_{j|i} \lambda(j) $
如果i不是完全平方数,那么会有奇数次幂,他的约数可以选这个质数的0次方和1次方、2次方和3次方……奇数部分的约数和偶数部分的约数的$\lambda(j)$值一个加一个减可以互相抵消。
如果i是完全平方数,每个次幂都是偶数,如1次方和2次方、3次方和4次方……可以互相抵消,最后剩下0次方,即$\lambda(1) = 1$。
因此,$\lambda(i) \sum\limits_{j|i} \lambda(j)$当i是完全平方数的时候加1,不是完全平方数的时候值为零。
这样,问题就转化成求1以内的完全平方数+2以内的完全平方数+3以内的完全平方数+…+n以内的完全平方数。
最后,我们可以考虑每个完全平方数的贡献,1共加n/1次,4共加n/4次……
