题目大意:给定一个整数n,求这个整数的第k大约数,如果约数不存在,输出-1。
You are given two integers n and k. Find k-th smallest divisor of n, or report that it doesn’t exist.
Divisor of n is any such natural number, that n can be divided by it without remainder.
The first line contains two integers n and k (1 ≤ n ≤ 1015, 1 ≤ k ≤ 109).
If n has less than k divisors, output -1.
Otherwise, output the k-th smallest divisor of n.
Input
4 2
2
5 3
-1
12 5
6
In the first example, number 4 has three divisors: 1, 2 and 4. The second one is 2.
In the second example, number 5 has only two divisors: 1 and 5. The third divisor doesn’t exist, so the answer is -1.
2 seconds 256 megabytes
解题思路
n是1015,很大,从1到1015逐个数字枚举会超时;但一个数n的约数,不超过2*√n个,因为不超过√n的约数最多√n个,超过√n的约数跟不超过√n的约数是一一对应的。
我们可以把不超过√n的约数全部求出来到数组a,如果共有m个,而且k不超过m,那么直接输出a[k],否则继续通过这m个约数,求得另外m个约数。
注意,如果n是平方数,那么约数个数为奇数;后面的约数是有可能超过int范围的;后面的约数,依次为n/a[m]、n/a[m-1]、n/a[m-2]……、n/a[m+1-k]、……,如果m+1-k小于0,那么不存在第k个约数。
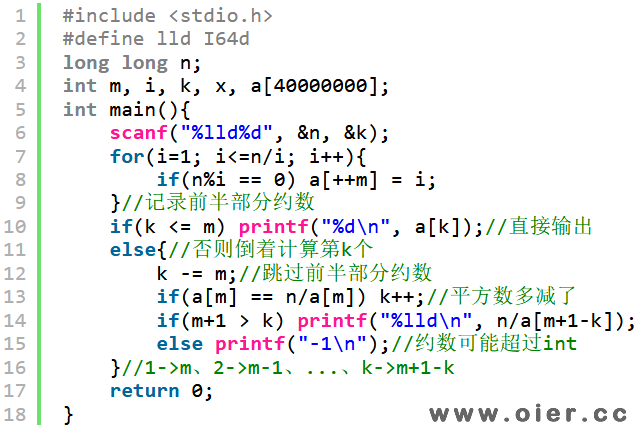
程序实现