题目大意:给定n个正整数,从中选出m个数,如果m>1的话这m个数的最大公约数不能为1,m最大是多少?
Bash has set out on a journey to become the greatest Pokemon master. To get his first Pokemon, he went to Professor Zulu’s Lab. Since Bash is Professor Zulu’s favourite student, Zulu allows him to take as many Pokemon from his lab as he pleases.
But Zulu warns him that a group of k > 1 Pokemon with strengths {s1, s2, s3, …, sk} tend to fight among each other if gcd(s1, s2, s3, …, sk) = 1 (see notes for gcd definition).
Bash, being smart, does not want his Pokemon to fight among each other. However, he also wants to maximize the number of Pokemon he takes from the lab. Can you help Bash find out the maximum number of Pokemon he can take?
Note: A Pokemon cannot fight with itself.
The input consists of two lines.
The first line contains an integer n (1 ≤ n ≤ 105), the number of Pokemon in the lab.
The next line contains n space separated integers, where the i-th of them denotes si (1 ≤ si ≤ 105), the strength of the i-th Pokemon.
Print single integer — the maximum number of Pokemons Bash can take.
3 2 3 4
2
5 2 3 4 6 7
3
gcd (greatest common divisor) of positive integers set {a1, a2, …, an} is the maximum positive integer that divides all the integers {a1, a2, …, an}.
In the first sample, we can take Pokemons with strengths {2, 4} since gcd(2, 4) = 2.
In the second sample, we can take Pokemons with strengths {2, 4, 6}, and there is no larger group with gcd ≠ 1.
2 seconds 512 megabytes
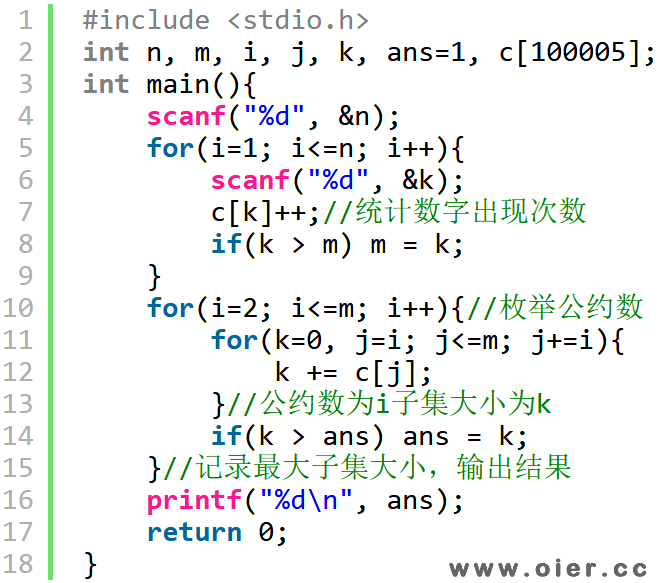
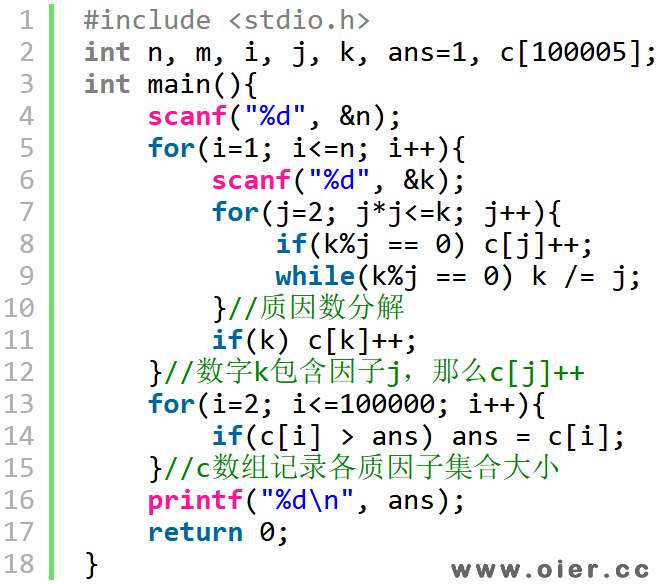
解题思路
统计每个约数可以选择数字的个数,即集合大小,输出最大值。
程序实现
分解质因数:没读入一个数,将将其分解质因数;每得到一个新的质因子j,那么c[j]++,表示选j为公约数,可以选择该数字。只需要统计质因子,因为其他因子可以选择的数字,质因子也可以选择;时间复杂度O(n√n)。
调和级数:统计10完以内各个数字出现的次数,然后枚举公约数,累加该约数可以选择的数字个数。
如公约数为2,需要累加c[2]、c[4]、c[6]……公约数是3,需要累加c[3]、c[6]、c[9]……
时间复杂度是O(nlogn),n/2+n/3+n/4+…+n/n = n * (1/2 + 1/3 + 1/4 + … + 1/n) = n * log(n)