题目大意:人选宠物或者宠物选人,都是选特点值最接近的;宠物收养场不断有领养者和宠物进来,如果同时存在宠物和领养者,那么就会领养;请问所有领养结束后特点值差的和是多少?
题目描述
凡凡开了一间宠物收养场。收养场提供两种服务:收养被主人遗弃的宠物和让新的主人领养这些宠物。
每个领养者都希望领养到自己满意的宠物,凡凡根据领养者的要求通过他自己发明的一个特殊的公式,得出该领养者希望领养的宠物的特点值a(a是一个正整数,a<2^31),而他也给每个处在收养场的宠物一个特点值。这样他就能够很方便的处理整个领养宠物的过程了,宠物收养场总是会有两种情况发生:被遗弃的宠物过多或者是想要收养宠物的人太多,而宠物太少。
被遗弃的宠物过多时,假若到来一个领养者,这个领养者希望领养的宠物的特点值为a,那么它将会领养一只目前未被领养的宠物中特点值最接近a的一只宠物。(任何两只宠物的特点值都不可能是相同的,任何两个领养者的希望领养宠物的特点值也不可能是一样的)如果有两只满足要求的宠物,即存在两只宠物他们的特点值分别为a-b和a+b,那么领养者将会领养特点值为a-b的那只宠物。
收养宠物的人过多,假若到来一只被收养的宠物,那么哪个领养者能够领养它呢?能够领养它的领养者,是那个希望被领养宠物的特点值最接近该宠物特点值的领养者,如果该宠物的特点值为a,存在两个领养者他们希望领养宠物的特点值分别为a-b和a+b,那么特点值为a-b的那个领养者将成功领养该宠物。
一个领养者领养了一个特点值为a的宠物,而它本身希望领养的宠物的特点值为b,那么这个领养者的不满意程度为abs(a-b)。
你得到了一年当中,领养者和被收养宠物到来收养所的情况,请你计算所有收养了宠物的领养者的不满意程度的总和。这一年初始时,收养所里面既没有宠物,也没有领养者。
输入输出格式
输入格式:
第一行为一个正整数n,n<=80000,表示一年当中来到收养场的宠物和领养者的总数。接下来的n行,按到来时间的先后顺序描述了一年当中来到收养场的宠物和领养者的情况。每行有两个正整数a, b,其中a=0表示宠物,a=1表示领养者,b表示宠物的特点值或是领养者希望领养宠物的特点值。(同一时间呆在收养所中的,要么全是宠物,要么全是领养者,这些宠物和领养者的个数不会超过10000个)
输出格式:
仅有一个正整数,表示一年当中所有收养了宠物的领养者的不满意程度的总和mod 1000000以后的结果。
输入输出样例
输入样例#1:
5 0 2 0 4 1 3 1 2 1 5
输出样例#1:
3 注:abs(3-2) + abs(2-4)=3, 最后一个领养者没有宠物可以领养。
解题思路
与《找朋友》、《营业额的统计》等题目不同的是,选择完最接近的元素后,该元素不能被其他人选择,即需要删除它;不仅如此,人可以领养宠物,但出现人多宠物少的情况,就会出现“宠物选人”;因此,题目不方便仅仅用双向链表来解决,用平衡树会比较合适。
set是用平衡树实现的数据结构,支持插入(值或指针、单个或区间)insert、删除(单个或区间)erase、查找find、是否存在count、大小size、求第一个≥的元素lower_bound、求第一个>的元素upper_bound等操作,第一个元素是begin,结束位置是end。一些简单的平衡树操作,都可以用set来实现。
如我们需要求最接近x的元素,那么我们可以先查找第一个≥x的元素,其指针是q:如果q是begin位置,说明全都≥x,*q即最接近的元素;如果q是end位置,说明全都小于x(没有≥x的元素),–q即最大值、最接近的元素;如果不在begin和end,说明在第2小到最大之间,另外一个可能是最接近的元素就是–q,比较这两个谁更接近即可做出选择。注意,迭代器指针可以++、–,却好像不能够+1、-1?
又如我们需要删除[x, y]范围的所有元素,可以先找到第一个≥x的位置p,再找出第一个>y的元素q,然后erase(p, q)即可,删除区间是[p, q);如果删除的区间是[x, y),那么q就是第一个≥y的元素,这样y就不会被删除了。
注意:set中不保存重复元素,如果已经有一个元素1,就不会再插入一个1了。需要了解更多用法,请访问set。
掌握了set的一般用法后,题目就非常简单了:两个set,一个存储领养者,一个存储宠物;一旦有人/宠物进入,如果宠物/人的set为空,那么就之间插入即可,等待配对;否则,选择宠物/人的set中最接近的元素进行配对、累加不满意程度、删除。
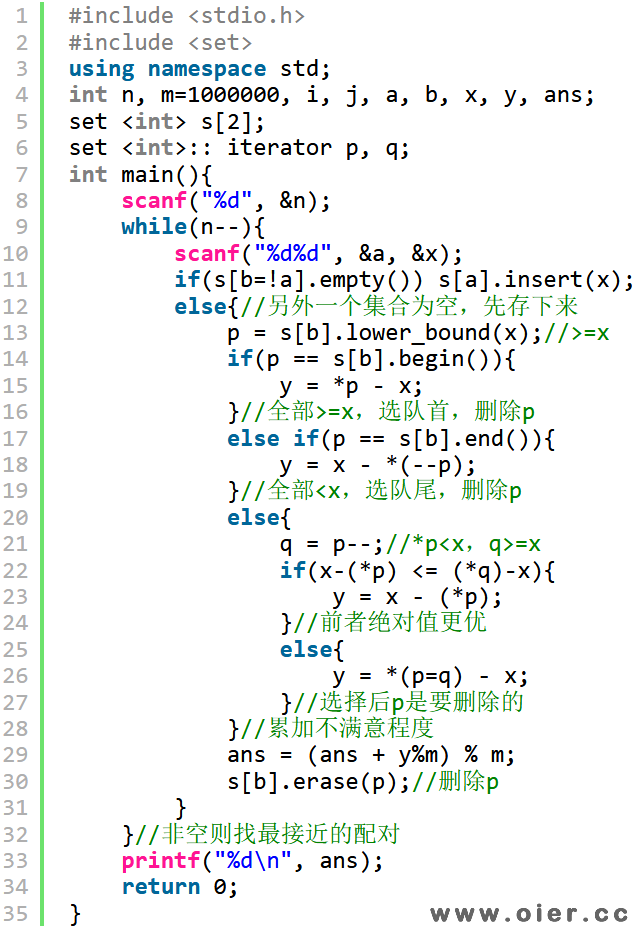
程序实现