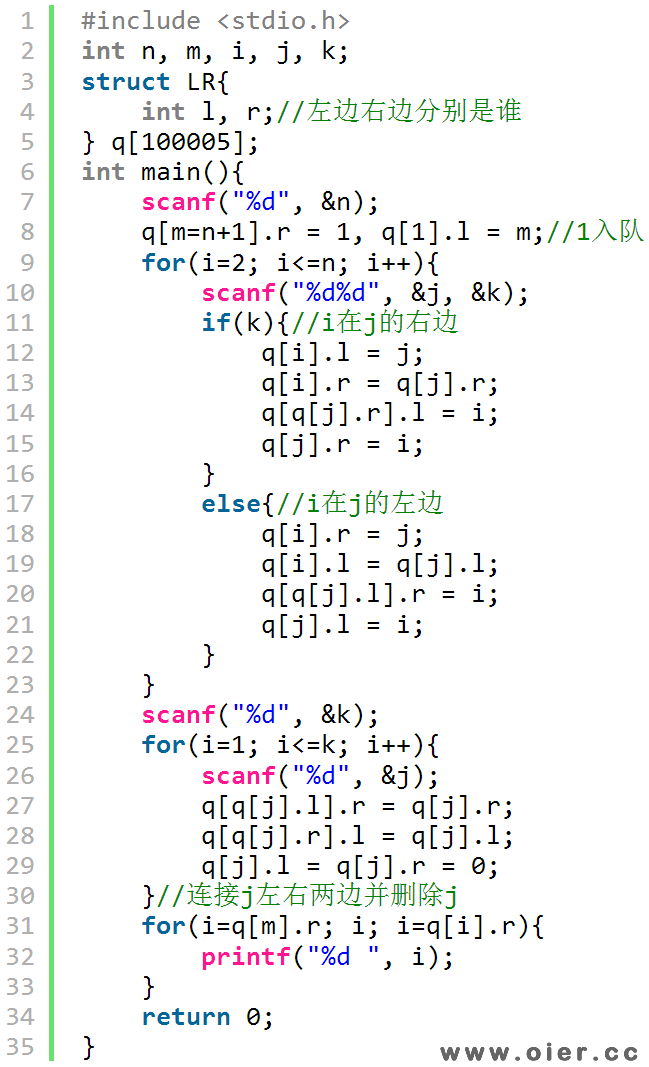
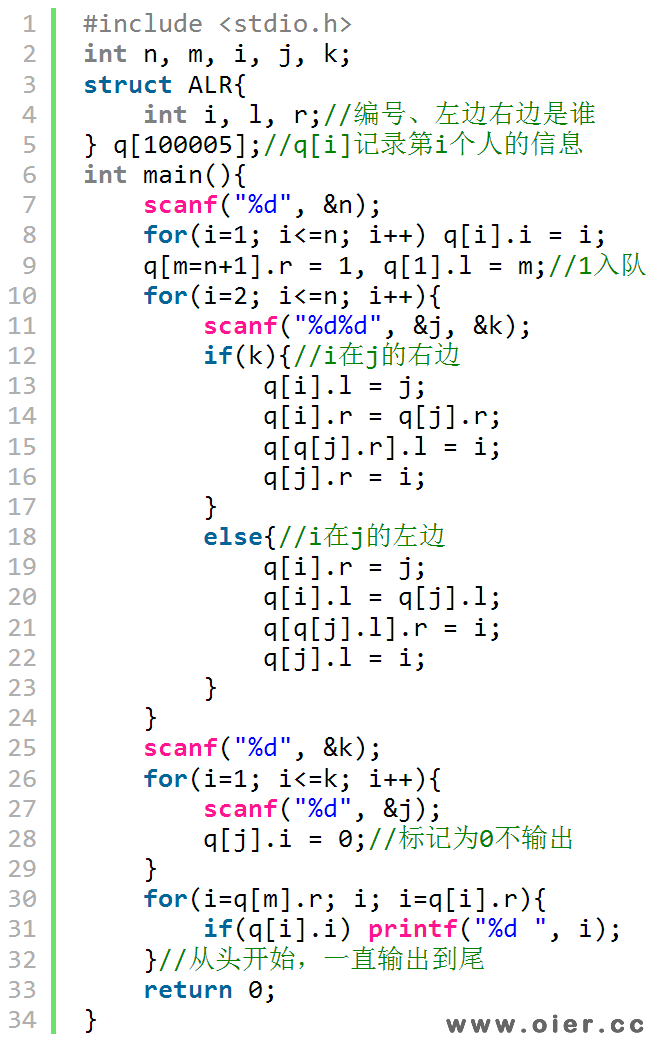
题目大意:编号为1到n的n个同学依次按照老师的指示入队,最后有m个同学出队,请问最后的队列是怎样的?
题目描述
一个学校里老师要将班上N个同学排成一列,同学被编号为1~N,他采取如下的方法:
1.先将1号同学安排进队列,这时队列中只有他一个人;
2.2~N号同学依次入列,编号为i的同学入列方式为:老师指定编号为i的同学站在编号为1~i -1中某位同学(即之前已经入列的同学)的左边或右边;
3.从队列中去掉M(M<N)个同学,其他同学位置顺序不变。
在所有同学按照上述方法队列排列完毕后,老师想知道从左到右所有同学的编号。
输入输出格式
输入格式:
输入文件arrange.in的第1行为一个正整数N,表示了有N个同学。
第2~第N行,第i行包含两个整数k,p,其中k为小于i的正整数,p为0或者1。若p为0,则表示将i号同学插入到k号同学的左边,p为1则表示插入到右边。
第N+1行为一个正整数M,表示去掉的同学数目。
接下来M行,每行一个正整数x,表示将x号同学从队列中移去,如果x号同学已经不在队列中则忽略这一条指令。
输出格式:
输入文件arrange.out仅包括1行,包含最多N个空格隔开的正整数,表示了队列从左到右所有同学的编号,行末换行且无空格。
输入输出样例
输入样例#1:
4 1 0 2 1 1 0 2 3 3
输出样例#1:
2 4 1 将同学2插入至同学1左边,此时队列为: 2 1 将同学3插入至同学2右边,此时队列为: 2 3 1 将同学4插入至同学1左边,此时队列为: 2 3 4 1 将同学3从队列中移出,此时队列为: 2 4 1 同学3已经不在队列中,忽略最后一条指令 最终队列: 2 4 1
说明
对于20%的数据,有N≤10;
对于40%的数据,有N≤1000;
对于100%的数据,有N, M≤100000。
解题思路
如果用数组存储,每次找到k号同学,时间复杂度是O(n),接着插入i号同学,需要移动数组,时间复杂度也是O(n),共有n次这样的操作,入队总的复杂度已经是O(n^2),必定超时。
如果用链表存储,每次找到k号同学,时间复杂度是O(n),接着插入i号同学,只需要改一下指针,改变k号同学附近的左右关系即可,时间复杂度是O(1),共有n次这样的操作,入队总的复杂度也是O(n^2),必定超时。
入队次数无法优化,那么如何才能降低查找k号同学的时间复杂度呢?结合数组和链表的优势,用数组存储这n个同学,第一个放在第一个位置,第二个放在第二个位置……这样查找只需要O(1);插入i号同学时,通过改变i号附近的左右关系,复杂度也是O(1),这样总体复杂度是O(n)。
最后是出队,可以把出队的同学都记录下来,输出的时候,看一下表里有没有他,有的话不输出即可;当然,用链表来删除也是很方便的。
程序实现