题目大意:在所有的n位数中,有多少个数中有偶数个数字3?由于结果可能很大,你只需要输出这个答案对12345取余的值。
输入
读入一个数n
输出
输出有多少个数中有偶数个数字3
样例输入
2
样例输出
73
提示
1<=n<=1000
样例说明:在所有的2位数字,包含0个3的数有72个,包含2个3的数有1个,共73个。
解题思路
先考虑递推关系,n位数,可以由n-1位数在最右边加一位得来(当然左边加也行,但要考虑前导零比较麻烦),加的数字是3,那么偶数个3变为奇数个3,奇数个3变为偶数个3;加的数字不是3(共9个),那么奇数个3还是奇数个3,偶数个3 还是偶数个3。不妨设f[n]表示n位数中奇数个3的数字个数,g[n]表示偶数个3的数字个数,那么f[n] = f[n-1]*9 + g[n-1],g[n] = g[n-1]*9 + f[n-1]。
接下来考虑初值:这种递推关系,是建立在没有前导零的情况下的,所以f[1] = 1,g[1] = 8。但最终g[1]好像应该是9吧?0也是一位数,偶数个3?
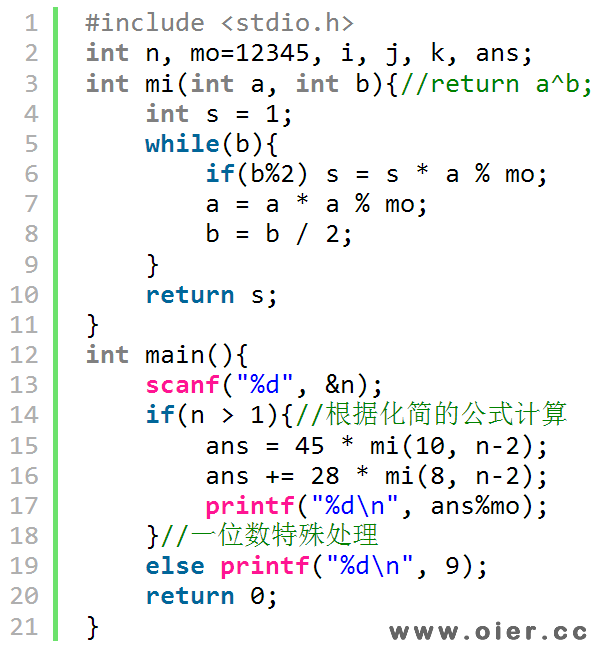
程序实现

优化一下:
f[n] + g[n] = 10 * (f[n-1] + g[n-1]) = 10 * 10 * (f[n-2] + g[n-2]) = … = 10 ^ (n-1) * (f[1] + f[1]) = 10 ^ (n-1) * 9
f[n] – g[n] = 8 * (f[n-1] – g[n-1]) = 8 * 8 * (f[n-2] – g[n-2]) = … = 8 ^ (n-1) * (f[1] – f[1]) = 8 ^ (n-1) * (-7)
两式相减可得:g[n] * 2 = 9 * 10 ^ (n-1) + 7 * 8 ^ (n-1)
即g[n] = (9 * 10 * 10 ^ (n-2) + 7 * 8 * 8 ^ (n-2)) / 2 = 45 * 10 ^ (n-2) + 28 * 8 ^ (n-2)