题目大意:一行n堆石子,每次可以从两端任意一堆取任意石子,最后不能取的算输,请问是否存在必胜策略?
题目描述
在研究过 Nim 游戏及各种变种之后,Orez 又发现了一种全新的取石子游戏,这个游戏是这样的:
有 $n$ 堆石子,将这 $n$ 堆石子摆成一排。游戏由两个人进行,两人轮流操作,每次操作者都可以从最左或最右的一堆中取出若干颗石子,可以将那一堆全部取掉,但不能不取,不能操作的人就输了。
Orez 问:对于任意给出一个初始一个局面,是否存在先手必胜策略。
输入输出格式
输入格式
文件的第一行为一个整数 $T$,表示有 $T$ 组测试数据。对于每组测试数据:
第一行为一个整数 $n$,表示有 $n$ 堆石子。
第二行为 $n$ 个整数 $a_1, a_2, \ldots , a_n$,依次表示每堆石子的数目。
输出格式
输入输出样例
输入样例 #1
1
4
3 1 9 4
输出样例 #1
0
说明
对于 $100 \%$ 的数据,$1 \le T \le 10$,$1 \le n \le 1000$,$1 \le a_i \le {10}^9$。
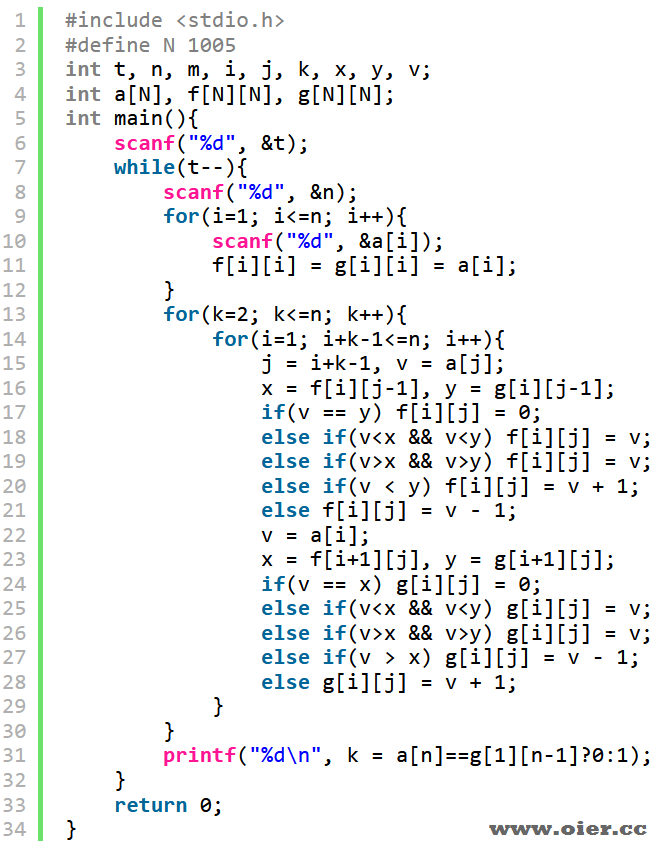
解题思路
设 f[i][j] 表示在 $[i,j]$ 区间的左侧放上一堆数量为 f[i][j] 的石子后,先手必败。(f[i][j] 可以为 0)即:$(f[i][j],a_i,a_{i+1},\cdots,a_j)$ 为必败局面,同理对右侧定义 g[i][j]。
f[i][j] 的唯一性证明:
假设 $f[i][j]$ 不唯一,则存在非负整数 $x_1,x_2(x_1 \neq x_2)$, $(x_1,a_i,a_{i+1},\cdots,a_{j-1},a_j)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},a_j)$ 均为必败局面。而这两个必败局面之间实际一步可达,故矛盾,进而原命题成立。
f[i][j] 的存在性证明:
假设不存在满足定义的 f[i][j],则对于任意非负整数 $x$,$(x,a_i,a_{i+1},\cdots,a_j)$ (记为 $A(x)$ 局面)为必胜局面。
由于 $A(x)$ 为必胜局面,故从 $A(x)$ 局面一步可达某个必败局面。
若拿最左边一堆,则不可能变成必败局面,因为这样得到的局面仍形如 $A$。(注意包括此行在内的接下来几行默认 $x \neq 0$)
于是设 $A(x)$ 一步可达的(某个)必败局面为 $(x,a_i,a_{i+1},\cdots,a_{j-1},y)$,显然有 $0 \le y < a_j$。
由于 $x$ 有无限个,但 $y$ 只有 $a_j$ 种——根据抽屉原理,必存在 $x_1,x_2(x_1 \neq x_2),y$ 满足 $(x_1,a_i,a_{i+1},\cdots,a_{j-1},y)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},y)$ 都是必败局面。但这两个必败局面之间实际一步可达,故矛盾,进而原命题成立。
只有一堆石子的时候,左边或者右边增加一堆相同大小的必败。
多堆石子,分类讨论。对于区间[i, j],前驱是[i-1, j]和[i, j-1],以f为例,设x=f[i][j-1],y=g[i][j-1]。
如果a[j]比x和y都小,那么a[i-1]跟他一样小,即f[i][j] = a[j],无论怎样都是必败的,因为后手一直维护两端相等,直到最后总会得到两端其中一个是0,另一个不是0,此时是可赢状态。
如果x <a[j] < y,令a[i-1] = a[j],此时发现能赢,因为先手总能让左端比右端大1,左端谁先取了<=x谁就输,右端谁先取了<x谁就输,所以一开始就应该让左端比右端大1,即f[i][j] = a[j] + 1,这样后手总能维护左端比右端大1。
如果y < a[j] < x,同理,左端谁先取了<x谁就输,右端谁先取了<=x谁就输,谁能维护左端比右端小1就能赢,即f[i][j] = a[j] – 1。
如果a[j]比x和y都大,谁先取到中间或者很小谁输,所以f[i][j] = a[j]即可,后手不断维护相等,直到最后出击获胜。
g[i][j]的证明与推导同理。
程序实现