
铜组A题:预处理右边最近的GH,分类讨论模拟。

铜组B题:积木大赛加强版的贪心,左边的调整好了,如果右边也需要,就顺便帮一下他。

铜组C题:爆搜写得好可以满分,记忆化搜索和动态规划稳拿满分。

银组A题:每头牛贪心选择最多的草,每段草至多被两头牛覆盖。尺取法预处理出每段草1头牛的覆盖量和2头牛的覆盖量(全部),最后逐头牛贪心选择即可。

银组B题:首先用并查集合并连通块,接着枚举两条边用在哪里,要么没有中转集合,只需要1条边;要么需要中转集合,需要2条边。最后利用set二分查找快速计算两个集合的最短距离。

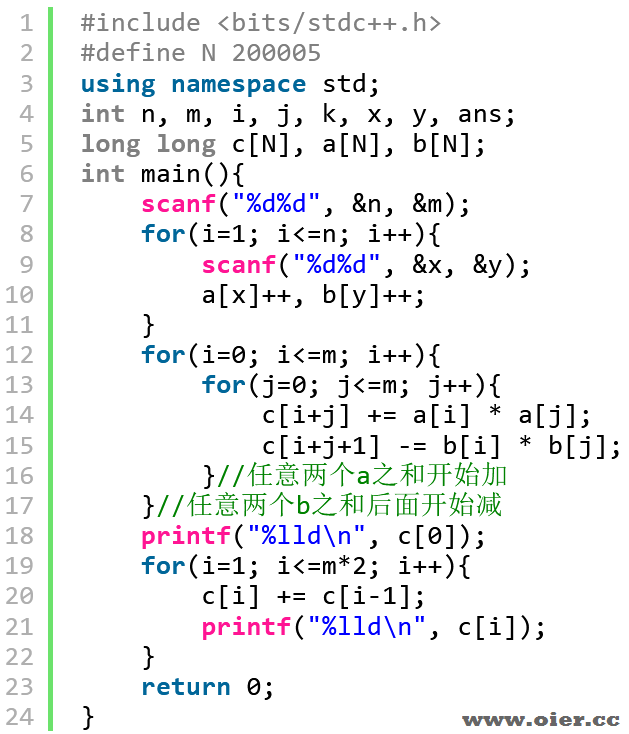
银组C题:枚举任意两个点,计算a之和、b之和,两个和之间的k都可以增加一种方案,可以使用差分数组提高效率。继续观察,m的范围小,a和b是可以分开处理的,与顺序无关,故可以使用桶排序、加乘原理优化。
金组A题:询问2是个需要贪心选择的DP,通过贪心来转移速度才会更快。暴力枚举每一头牛是否匹配,如果匹配,那么他只需要和右边第1头牛、右边第2头牛匹配,往后匹配是多余的,因为他可以跟第1头牛匹配,让第2头牛往后匹配,从而实现等价转换。暴力后改记忆化搜索可以顺利满分。(跟银组第一题一样,每一段不连通的牛可以单独处理。)

金组B题:枚举说HI的位置i,通过思考分析发现,之前比a[i]大的数,必然说HI,否则此时跳过而不是说HI;之前比a[i]小的数,必然说LO,否则此时跳过而不是说HI。那么,下一次说LO的位置可能在哪里?不妨设之前说LO的数字中最大的为x,那么后面最近的在(x, a[i])范围的数字就是说LO的位置,因为太大的和太小的均跳过了。分块二分查找出这个位置,这样就转化成银组第三题的差分问题了。每个可能的HI位置都处理好,答案也就出来了。

之所以打出分块代码,是因为张某某告诉我,题目时限是4s,我还以为放宽限制了,原来是他没留意语言!set分块二分4s左右,没过还以为是USACO评测机慢,改为数组分块二分3秒左右,结果还是超时,最终改为双分块险过!早知道时限2s,就打线段树了。

金组C题:看似一道几何数学题,实际上就是一道模拟构图题。不合法情况无非几种,首先是断开,某种颜色在a出现,在a+1没出现,但又在a+2出现了;其次是交叉,一种颜色被包含,就永远要被包含。我们可以将颜色拆点,1~n表示下边,n+1~n+n表示上边,用邻接矩阵存储他们之间的关系,最后暴力枚举每一种颜色是否出现交叉、是否完全被包含即可。
