题目大意:n个点,m种类型,某些类型直接可以连通,代价是他们编号的差值,请问从点1走到点n,至少花费多少代价?
小明正在研究真菌X的孢子传播特性。
他准备了一排连续n块不同质地的土壤(共k种,其中第m块土壤土质为q[m]),观察真菌X如何从第1块土壤蔓延到第n块。很快他发现了真菌X的两个传播特点:
(1)真菌X从第u块土壤释放孢子到第v块土壤,需要吸收|u-v|摩尔的营养液;
(2)真菌X的孢子到达一块土壤并扎根后,无需营养液即可成长。但它会对当前土壤的土质产生一定的适应性,这将导致这块土壤的真菌X新释放的孢子无法在某些质地的土壤上扎根。
小明记录下了真菌X对不同土质适应性的数据,记为S(i,j)。S(i,j)=1表示在第i种土质下的真菌X的孢子能够在第j种土质中扎根,S(i,j)=0则表示不能。(不保证S(i,i)一定为1)
现在小明想知道,真菌X从第1块土壤蔓延到第n块土壤,至少需要提供多少摩尔的营养液?
输入
第一行输入两个正整数n,k; 第二行输入n个正整数表示每块土壤的土质种类q[m]; 之后k行,每行一个k位长度的01串,其中第i行第j个数表示S(i,j);
输出
输出一个正整数,表示真菌X从第1块土壤蔓延到第n块土壤所需营养液的最小值。 如果不能从第1块土壤蔓延到第n块土壤,输出 -1。
数据范围
对于23%的数据,2<=n<=10;
对于38%的数据,2<=n<=1000;
对于100%的数据,2<=n<=50000,1<=q[m]<=k<=50,S(i,j)∈{0,1};
输入样例
5 4 1 4 2 3 4 1010 0001 0110 0100
输出样例
6
样例解释
由数据可知,第1块土壤的孢子只能传到第4块土壤(土质1→3),第2块土壤的孢子只能传到第3块土壤(土质4→2),第3块土壤的孢子只能传到第2、5块土壤(土质2→4),第4块土壤的孢子只能传到第3块土壤(土质3→2)。最优蔓延顺序为 1→4→3→5。总营养液消耗为 |1−4|+|4−3|+|3−5|=6。
解题思路
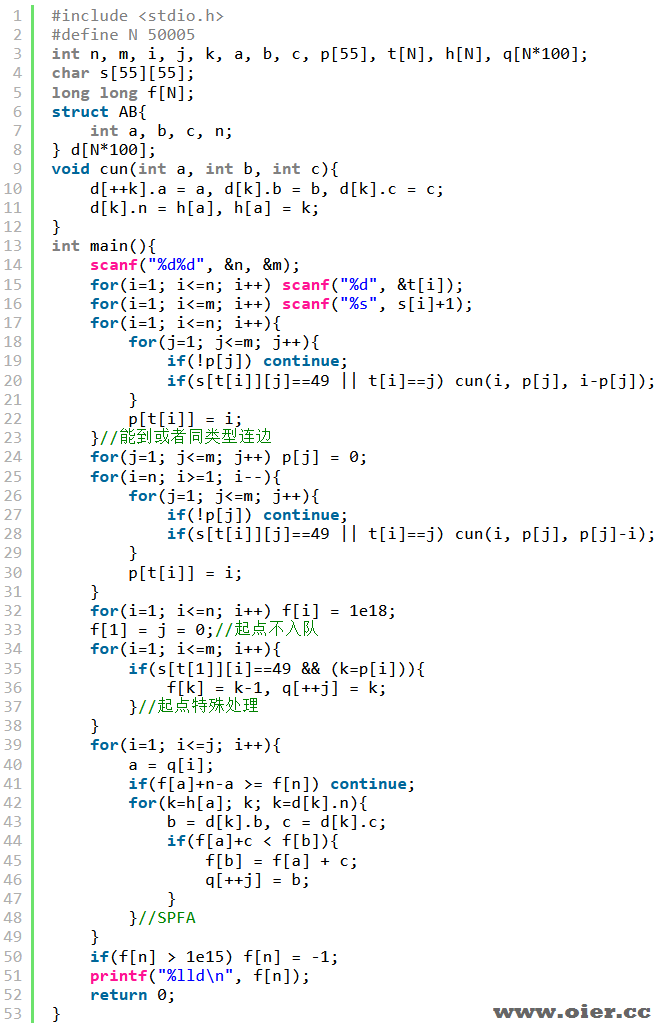
每个点至多可以建n条边,全部存储比对存不下、超时,对于同一种类型,能不能考虑只存储最近的点呢?这样只需要对相近的同种颜色连边即可实现传递,这样每个点至多往左50条边,往右50条边,总计500万条边,是可行的。
但这样有一个问题,如果本身同类型不能走,会不会出错呢?虽然自己类型不能到自己类型,但只要通过其他点到达过,就相当于可以自己到自己了。只有起点未通过中转,需要特殊处理一下而已。
起点不入队,直接使用S数组扩展出能到的点入队即可。当然,起点如果不能到同类型点,它的同类型边不连也行。
程序实现