题目大意:一份奖品需要包括n个物品,每个物品需要$x_i$件,已知这些物品的两种包装的价格和费用,m元至多可以凑出多少件奖品?
题目描述
学校刚开完运动会,准备为尽可能多的同学评奖,并为每个人颁发一份奖品。一份奖品包括 $N$ 个物品,如:$5$ 支铅笔、$10$ 本练习薄等。每份奖品完全一样。虽然学校的保管室里还有一些办去年运动会后剩余的物品。在商店里,每种物品都有很多,但是,只有两种包装:大盒或小盒,并且不拆开买。
现在的问题是,充分利用这 $M$ 元钱,最多可准备多少分这样的奖品?
输入输出格式
输入格式
第一行两个整数:$N,M$。
下面有 $N$ 行,每行有六个正整数 $x,y,sm,pm,sv,pv$,分别表示一种物品的相关数据:
* $x$,一份奖品中,这种物品需要的件数。
* $y$,这种物品去年剩余的件数。
* $sm$,这种物品小包装的件数。
* $pm$,这种物品小包装的一盒价格。
* $sv$,这种物品大包装里的件数。
* $pv$,这种物品大包装的一盒价格。
输出格式
输入输出样例
输入样例 #1
2 100
10 8 10 10 13 11
12 20 6 10 17 24
输出样例 #1
5输入样例 #2
3 65
10 5 7 10 13 14
10 5 8 11 14 15
10 5 9 12 15 16
输出样例 #2
2说明
对于全部的数据,满足:
$1 \le N \le 100$,$1 \le M \le 10^5$。
$10 \le x, pm \le 100$,$1 \le y, sm \le 100$,$sm < sv \le 100$,$pm<pv\le 100$。
解题思路
显然,奖品份数越多,需要的钱就越多。我们可以二分答案,贪心求最小费用。
已知奖品份数k,那么每样物品都知道需要多少件,求每样物品的费用的独立的,我们可以枚举大包装买多少件,打擂台求出最小费用,n个物品的费用加起来,即k份奖品的最小费用,费用太高,份数只能降低,否则尝试更多奖品。
奖品份数最小是0,最大是m*10+10,因为至多可以买m*100件,至少10件组成一份奖品,去年至多剩下100件。
优化1:计算每种物品至多凑出多少份奖品,总价为m,全买小包的,按大包的数量算。
优化2:计算费用的时候,发现费用超过m,后面没必要继续算了,这样遇到大包装数量很少,也可以避免超时。
数据说都是正整数,感觉是有0存在的,可能不需要某件物品呢,代码20行就是为了避免运行错误!
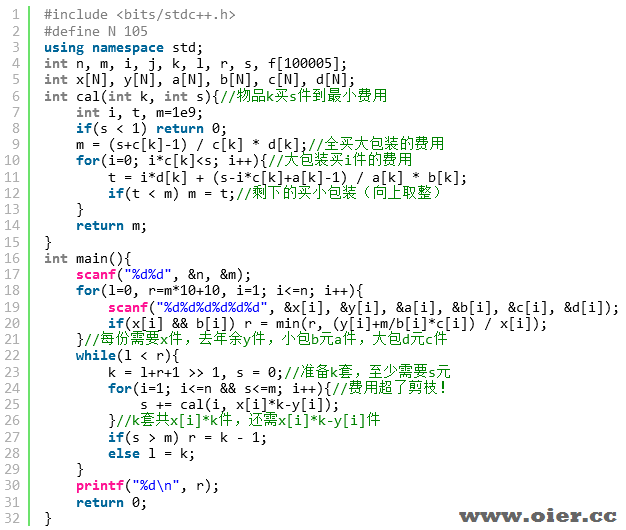
程序实现