题目大意:n个数,取其子序列组成奇数位相同、偶数位也相同的数列,长度最大是多少?
题目描述
Z同学近期喜欢上了数字序列。然而他发现了一种新的序列。把这个序列成为Z序列。
Z序列可以表示为:
1、$A_1 = P$ , P可以是任何一个整数
2、$A_i = A_{i-1} + (-1)^{i+1} * Q (i > 1) $, Q可以是任何整数
现在Z同学有个序列,长度为N 。整个序列由N个整数组成。
现在请你帮Z同学找出最长的Z序列。
提示:如果B序列删除若干元素可以得到S序列,那么S序列就是B的子序列。
输入
第一行输入一个N(N <= 5000) 接下来的1行总共有N个数字,代表序列的元素,分别是B1,B2,B3…..Bn。
输出
输出一个整数,代表B序列当中的最长的Z序列的长度。
样例输入
样例1:
2
3 5
样例2:
4
10 20 10 30
样例输出
样例1:
2
样例2:
3
提示
n的范围:1, 10, 30, 50, 100, 300, 500, 1000, 3000, 5000, 5000
其他数据不超过n*8。
样例1:样例1 本身就是一个Z序列,所以长度是2
样例2:10,20,10 符合Z序列,所以最长为3
解题思路
方法一:链表合并
将相等的数字用链表链起来,按照一定的顺序连接即可。注意,需要交替选择,如果连续若干个A都在B的左边,那么只能选择一个A,其他A扔掉。时间复杂度为$O(n^2)$,虽然每一条链,最长为n,至多遍历n次,但均摊下来,复杂度没那么高。最终的效果,就是任意两个不同的数字,都会扫一遍他们的链表。假设有x种数字,那么每个链表被扫描x遍。如果共有y个链表,那么x+y <= 2n,最极端情况是x = y = n。
方法二:贪心动态规划
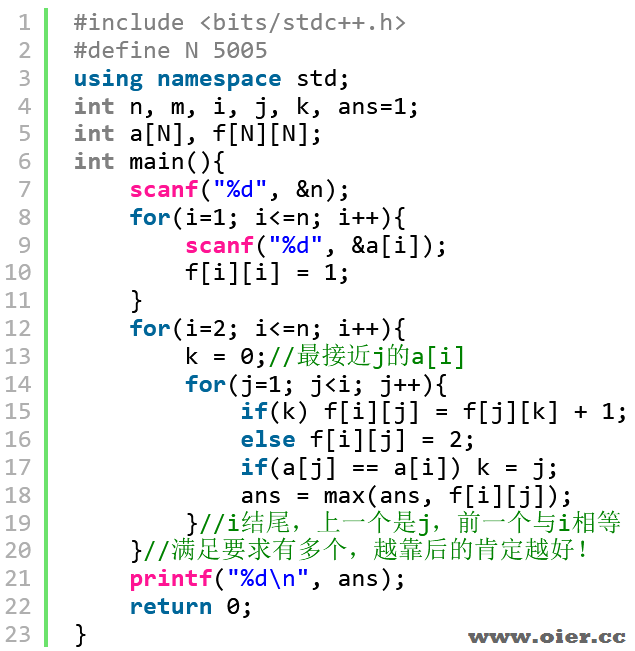
因为需要“接龙”,所以状态定义一般会包含“结尾”。交替序列,结尾有2个不同的数字,定义f[i][j]表示以i结尾,上一个是j的最优值,那么再上一个位置k,必然有a[i] == a[k],三重循环枚举可得大部分分,贪心一下即满分:k的位置越靠近j越好,因为前面更好转移、长度更大。
程序实现
离散化后,速度更佳:

暴力DP大部分分:

j从小到大枚举,顺序记录最接近的跟a[i]相等的位置k。