题目大意:一个环形字符串,只有2中字符,相同字符可以连线,要求连线不相交,最多连多少条线?
题目描述
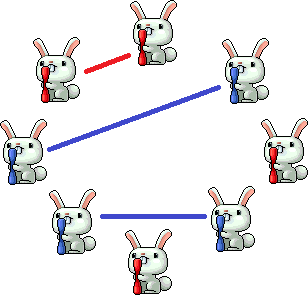
迷途竹林的兔子们玩起了一个游戏。首先,兔子们绕成一个环。每只兔子随机捡起红色或者蓝色的木棒。
紧接着,拿着相同颜色木棒的兔子可以把他们的木棒连接起来。显然,每只兔子只能连接到另一只兔子。同时,木棒相交是不被允许的。这样,总有一些兔子无法和其他兔子连接起来。
绕着手下的兔子们转了几圈之后,因幡帝突然想知道,最多能有多少对兔子连接起来。
输入
输出
样例输入
RRBRBRBB
样例输出
3
提示
样例解释:
•对于分值为 40 的子任务 1,保证兔子数 ≤ 10
•对于分值为 20 的子任务 2,保证兔子数 ≤ 100。
•对于分值为 40 的子任务 3,保证兔子数 ≤ 500。
解题思路
跟括号匹配一样,相邻能匹配的先匹配,因为这样匹配对其他括号并没有任何影响。
字符匹配也是一样的道理,相邻相同连线是最优的选择,连线后相当于消去他们,并且没有浪费任何一个字符,所以连续多个相同也是正确的,连续两个就更加正确了。
用栈进行类似“括号”匹配的操作,最终剩下的字符串要么是奇数n个字符——RB……BR,首位配对用一个字符用不了,答案是n/2已是最优;要么是偶数n个字符——RB……RB,必然不能全部配对,去掉一个字符按奇数配对,可以得到(n-1)/2对,也是最优。
综上所述,能配对直接配对,剩下的不能全部配对,但不管是奇数还是偶数,都能配出(n-1)/2对。
程序实现

DP做法:首先拉成一条链,对于每一个区间的配对数量,可以从任意位置切分。
区间[l, r],要么是首位配对,要么是中间位置切开,取最优值。
1、为什么每个区间都可以首尾配对?
因为每个区间配对完可以“消去”,不影响外面字符的配对。
2、为什么首尾能配对就是最优的?
相邻2个配对可以直接消去,不跨过其他字符,不浪费任何一个字符。
3、代码第11行不return会超时?
对的,会超时,记忆化搜索,状态有1000*500个,里面还有一重500的循环,时间复杂度会超时。
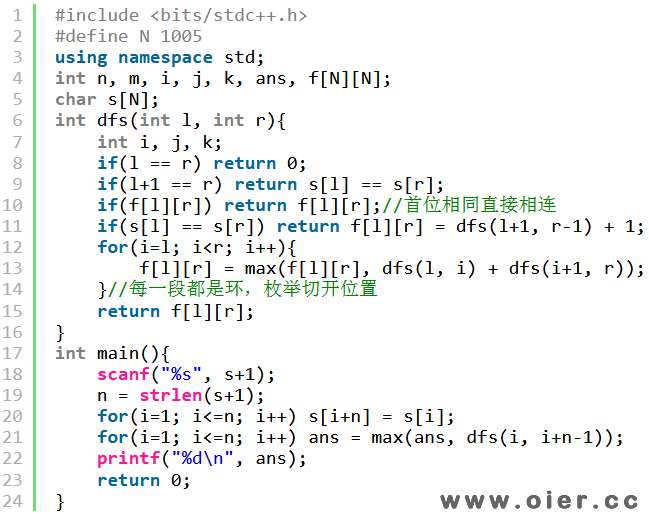
使用模来处理环,从0开始存储,如f[2][n+1]存储到f[2][1],如果代码第14行不写return:用模运算还是会超时;用判断加减法可以提高分数,运气好可以拿满分。