题目大意:六边形铺地砖,中间那块编号是1,之后从里往外按照顺时针顺序编号,问其中两个地砖之间隔着多少块地砖?
题目描述
当玛艾露贝莉·赫恩醒来的时候,她已经到达了空间站的内部。
空间站的地面由若干个六边形拼接起来。为了防止迷路,莲子使用顺时针的顺序,将六边形依次标上了号码,如图所示。
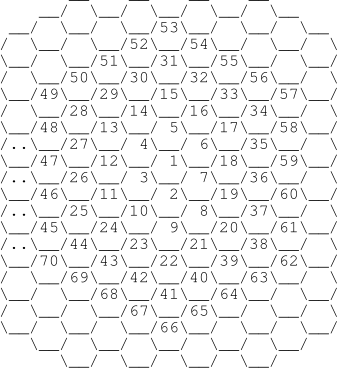
两个区域的距离,被定义为从其中一个区域到另一个最少需要经过多少个区域。
在空间站中穿梭的过程中,赫恩突然想要返回某个特定的位置。为了确认自己计算距离的设备在穿梭的过程中没有损坏,她希望你帮忙确定这两个位置之间的距离。
输入
输出
样例输入
19 30
样例输出
5
提示
•对于分值为 40 的子任务 1,保证 X, Y ≤ 10
•对于分值为 20 的子任务 2,保证 X, Y ≤ 1000。
•对于分值为 40 的子任务 3,保证 X, Y ≤ 10000。
解题思路
解法与2014年螺旋矩阵相似,难度更大,关键在于如何计算每个数字的位置,其次是知道位置,如何计算他们的距离?
这两个问题都有难度,只要有一个想不出来,都很难得满分,这时就应该暴力40分——预处理10个数字任意两个之间的距离(可以从图中直接看出)。
首先是数字的位置:一开始比较难想,那就从简单的来:
1、在哪一圈:我们可以预处理出前i圈的数字数量,保存到a[i],数字在哪一圈,可以用查找算法,查找第一个大于等于数字的a[i],那么该数字在第i圈。
2、在哪一行:1为第0行,从左到右行数递增编号,不难发现每一圈最后一个数字的行号就是圈号。确定数字的圈号k,暴力找出他在哪一条边,根据规律就可以得出行号了——右边那条边,有k个数字,只有数字≥a[k]-k,那么数字行号不变等于k;否则如果数字≥a[k]-k*3,那么数字在上面两条边,数字每减少1,行号就会减少1……
3、在哪一列:同样的,1为第0列,从上往下递增编号。列会有半列,那就乘以2避免出现小数。六条边的规律是圈尾数字为第k列,逆时针六条边的编号规律是-2、-1、+1、+2、+1、-1。
其次是计算距离:举几个例子,看一下怎么走最快。同一列,直接往下走,步数等于列的差;同一斜,直接斜着走,步数等于行的差;同一行,斜上斜下交替走,步数等于行的差;行差大于列差:在“横着走”的过程,一定可以先走到该列(同一行),所以步数等于行差;列差大于行差:先斜着走到同一行,往直着走过去,步数等于行差+(列差-行差)/2,因为往下走,列-2。
本题的行列编号,既不是按“行列”,也不是按坐标,因为1、7、19、37、61的行列比较有规律。
程序实现

用直角坐标系的坐标来进行定位,第m圈的末尾数字的坐标是(m, -m),6个方向预处理到数组:

如果觉得贪心不正确,可以多举例子证明,穷举证明,或者换一种广搜的方法:
