题目大意:已知n个小朋友手上的数字,根据数字计算特征值,进而计算分数,输出最大分数。
题目描述
有n个小朋友排成一列。每个小朋友手上都有一个数字,这个数字可正可负。规定每个小朋友的特征值等于排在他前面(包括他本人)的小朋友中连续若干个(最少有一个)小朋友手上的数字之和的最大值。
作为这些小朋友的老师,你需要给每个小朋友一个分数,分数是这样规定的:第一个小朋友的分数是他的特征值,其它小朋友的分数为排在他前面的所有小朋友中(不包括他本人),小朋友分数加上其特征值的最大值。
请计算所有小朋友分数的最大值,输出时保持最大值的符号,将其绝对值对p取模后输出。
输入
第一行包含两个正整数n、p,之间用一个空格隔开。
第二行包含n个数,每两个整数之间用一个空格隔开,表示每个小朋友手上的数字。
输出
输出只有一行,包含一个整数,表示最大分数对p取模的结果。
样例输入
[Sample 1]
5 997
1 2 3 4 5
[Sample 2]
5 7
-1 -1 -1 -1 -1
样例输出
[Sample 1]
21
[Sample 2]
-1
提示
【样例说明】
样例1小朋友的特征值分别为1、3、6、10、15,分数分别为1、2、5、11、21,最大值21对997的模是21。
样例2小朋友的特征值分别为-1、-1、-1、-1、-1,分数分别为-1、-2、-2、-2、-2,最大值-1对7的模为-1,输出-1。
【数据范围】
对于50%的数据,1≤n≤1,000,1≤p≤1,000所有数字的绝对值不超过1000;
对于100%的数据,1≤n≤1,000,000,1≤p≤10^9,其他数字的绝对值均不超过10^9。
NOIP2013普及组第三题
解题思路
1、根据题目意思,一步一步来避免出错,先记录数字a[i],再计算特征值。
2、特征值的计算,最简单就是暴力去算,枚举所有可能的区间,求区间和,记录最大值,至少时间复杂度O(n*n*n)。用前缀和优化,可以降低到O(n),具体方法如下:
1)连续一段的和,用变量s来记录,每遇到一个数字a[i],累加起来,因为要求最大值,所以如果发现s是负数,清零即可,因为后面的数字加负数不会变大!
2)特殊情况:如果全是负数,前面的是-1,后面的是-2,那么最大值是-1,前面的-1清零会导致最大值为0。不难发现,后面的特诊征,大于等于前面的特征值,b[i-1]是i-1的特征值,包含了前面所有连续区间的最大值,还差以a[i]结尾的而已。s记录的正是以a[i]结尾的最大值,两者去最大值就行。
3、计算分数:一种是直接模拟计算,但会爆long long;一种是用数学方法优化,可以得满分。
程序实现
模拟算分数:预处理第一个小朋友的分数,用s记录最大分数,递推出后面每个小朋友的分数。因为s最大值是1000000*int,n个这样的s加起来会爆long long,所以无法得到满分,实测80分。
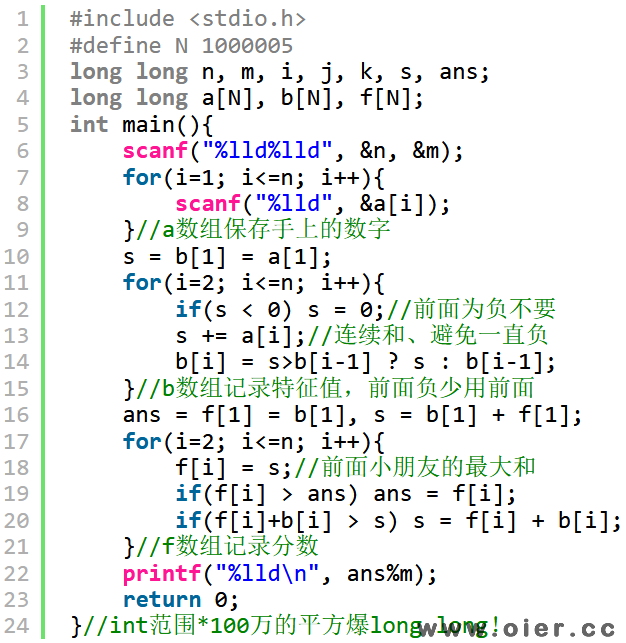
题目要求输出的是取模的结果,可不可以中间取模呢?不可以!
如果首项是一个很大的负数,且后面加起来也不够他变正数,取模后影响正负性。
既然不能中间过程取模,难度要用高精度?找到规律就不需要!
分数只跟第一个小朋友的分数和各个小朋友的特征值有关:后面小朋友的分数,等于第一个小朋友的分数加上若干个特征值,是正数当然加越多越好!需要注意的是,要加特征值,就必须加上第一个小朋友的特征值,如果特征值之和大于0,那就加,否则不加。
