SSOJ1081滑雪课程设计[USACO]
2246+
作者:crxis 发布:2018-09-20 分类:枚举
题目大意:n座山,要让最高和最低的山相差不超过17,最少要花费多少?(改变高度需要花费平方价格)
题目描述
农民约翰的农场里有N座山峰(1<=N<=1000),每座山都有一个在0到100之间的整数的海拔高度。在冬天,因为山上有丰富的积雪,约翰经常开办滑雪训练营。
不幸的是,约翰刚刚得知税法在滑雪训练营方面有新变化,明年开始实施。在仔细阅读法律后,他发现如果滑雪训练营的最高和最低的山峰海拔高度差大于17就要收税。因此,如果他改变山峰的高度(使最高与最低的山峰海拔高度差不超过17),约翰可以避免支付税收。
如果改变一座山x单位的高度成本是x^2单位,约翰最少需要付多少钱?约翰只愿意改变整数单位的高度。
输入
第一行:一个整数n
第二行到N+1行:每行是一座山的海拔高度
输出
约翰需要支付修改山海拔高度的总金额,最高和最低的山峰间高度差最多17。
样例输入
5
20
4
1
24
21
样例输出
18
解题思路
枚举高度区间,如果最低高度是x,那么x的范围是0到93,最高高度y的值是x+17,每次枚举,如果发现有山超过最高高度或者低于最低高度,就需要改变高度累加费用。
枚举所有可能的区间后,计算并记录最小费用即可。
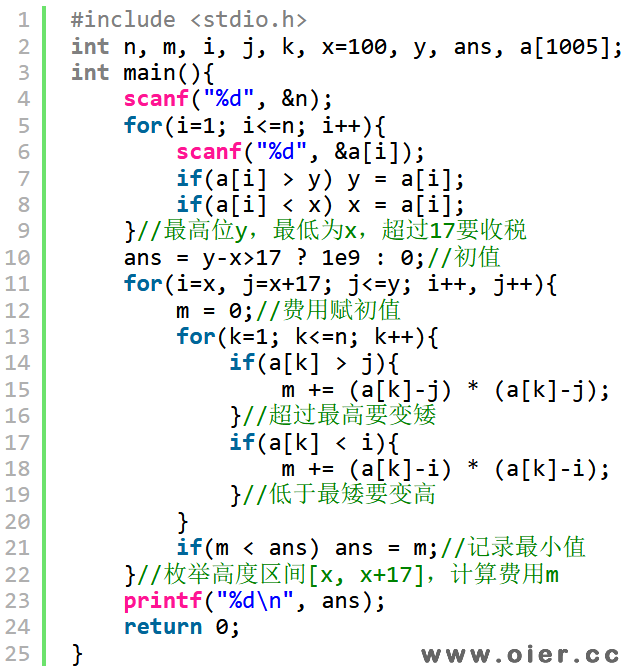
程序实现