SSOJ1076修理牛棚[USACO]
2760+
作者：crxis 发布：2018-09-11 分类：贪心
题目大意：有n个牛棚需要修理，只能买m块木板，购买的木板最小长度和是多少？
题目描述
在一个夜黑风高,下着暴风雨的夜晚,Farmer John的牛棚的屋顶、门被吹飞了。 好在许多牛正在度假，所以牛棚没有住满。 牛棚一个紧挨着另一个被排成一行，牛就住在里面过夜。 有些牛棚里有牛，有些没有。 所有的牛棚有相同的宽度。 自门遗失以后,farmer John必须尽快在牛棚之前竖立起新的木板。 他的新木材供应商将会供应他任何他想要的长度,但是吝啬的供应商只能提供有限数目的木板。 Farmer John想将他购买的木板总长度减到最少。
给出:可能买到的木板最大的数目M(1<= M<=50);牛棚的总数S(1<= S<=200); 牛棚里牛的总数C(1 <= C <=S);和牛所在的牛棚的编号stall_number(1 <= stall_number <= S),计算拦住所有有牛的牛棚所需木板的最小总长度。 输出所需木板的最小总长度作为答案。
输入
- 第 1 行: 木板最大的数目M ,牛棚的总数S 和 牛的总数C(用空格分开)
- 第 2 到 C+1行: 每行包含一个整数，表示牛所占的牛棚的编号。
输出
单独的一行包含一个整数表示所需木板的最小总长度。
样例输入
4 50 18
3
4
6
8
14
15
16
17
21
25
26
27
30
31
40
41
42
43
样例输出
25
解题思路
最好的就是每个牛棚用一块长度为1的木板，但是木板数量有限可能无法实现。
如果只买m块木板，那么中间肯定有m-1个间隔（如果无间隔就可以用同一块木板），长度之和就等于总长度减去间隔之和，怎么让间隔之和最大呢？
去最大的m-1个间隔！
首先读入牛棚位置，排序后将牛排之间的间隔保存到b数组，最间隔排序，选最大的m-1个间隔。
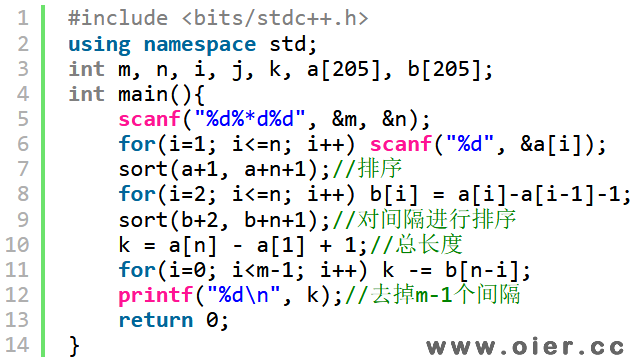
程序实现
