题目大意:一条路上有n棵香蕉树,树上香蕉数为ai,猴子在第一棵树上,已知香蕉树的位置,以及猴子每次跳的最远距离m,请问只允许条c次,猴子最多能迟到多少香蕉?
题目描述
一只猴子找到了很多香蕉树,这些香蕉树都种在同一直线上,而猴子则在这排香蕉树的第一棵树上。这只猴子当然想吃尽量多的香蕉,但它又不想在地上走,只想从一棵树跳到另一棵树上.同时猴子的体力有限,它不能一次跳得太远或跳得次数太多,每当他跳到一棵树上,就会把那棵树上的香蕉都吃掉。那么,它最多能吃多少个香蕉呢?
输入
输入第一行为三个整数,分别是香蕉树的棵数N,猴子每次跳跃的最大距离D,最多跳跃次数M.
下面N行每行包括两个整数,ai,bi分别表示每棵香蕉树上的香蕉数,以及这棵树到猴子所在树的距离。输入保证这些树按照从近到远排列,并且没有两棵树在同一位置。b0总是为0 .
输出
输出只有一行,包含一个整数,为猴子最多能吃到的香蕉数。
样例输入
5 5 2
6 0
8 3
4 5
6 7
9 10
样例输出
20
提示
n和m在10个点的数据范围:5, 10, 100, 300, 500, 800, 1000, 2000, 3000, 4000, 5000;d不超过20000
解题思路
状态定义:f[i][j]表示至多条j次,最后跳到第i棵树,能够吃到的最大香蕉数量,f[1][0]=a[1],因为猴子在第1棵树上,不需要跳就能吃掉香蕉。
状态转移:先至多算1次,跳到各棵树上的最大香蕉数,再算至多2次、3次……直到c次。f[i][j] = f[k][j-1] + a[i],取最大值。当前树是i,前一棵树是k,需要再跳一次,那么到i是j次,到k就是j-1次,跳了之后,可以吃掉第i棵树的香蕉a[i]个。
暴力代码无法拿到满分,但完美可以继续优化。首先是降维优化,可多得10分。在转移过程中,只会用到前1次的数据,我们可以用滚动数组,或者直接降维。具体方法:我们就f[i]的时候,需要用到前一次的f[j](j<i),那么只需要保证,在求f[i]的时候,f[j]还是前一次的f[j]就行,即从后往前DP,先求新的f[n],再求f[n-1]、f[n-2]……这样,就保证用到的前面的f[j]还未被更新。
单调队列优化:看到区间平移求最大值,不难想到单调队列优化。逐个f[j]入队,如果发现队尾的值比前一个大,那么前一个就不会用到了,因为如果选它,还不如选值更大的队尾,即队尾要最小,维护单调递减的队列,这样每次只需要选择队头进行转移。当然,队头也有过期的时候,如队头的编号大于等于i,是不行的,因为f[i]只能选择i前面的树。
线段树求区间最大值:可以写,但并不方便,因为可能还需要二分求出区间的左端点。
程序实现
暴力DP:

降维优化:
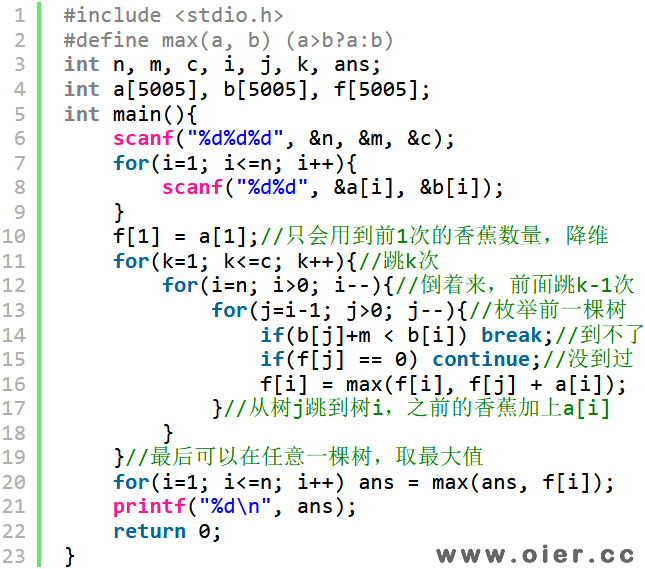
单调队列优化:
