题目大意:一个超时24小时营业,不同时间需要的出纳员数目不同,现有n个人过来应聘,已知各个时间点需要的人数,以及应聘任意开始工作的时间点,请问至少需要聘用多少人?
题目描述
一家每天24小时营业的超市,需要一批出纳员来满足它的需要。超市经理雇佣你来帮他解决问题:超市在每天的不同时段需要不同数目的出纳员(例如:午夜时只需一小批,而下午则需要很多)来为顾客提供优质服务。他希望雇佣最少数目的出纳员。
经理已经提供你一天的每一小时需要出纳员的最少数量——R(0), R(1), …, R(23)。R(0)表示从午夜到上午1:00需要出纳员的最少数目,R(1)表示上午1:00到2:00之间需要的,等等。每一天,这些数据都是相同的。有N人申请这项工作,每个申请者I在24小时中,从一个特定的时刻开始连续工作恰好8小时,定义tI (0 <= tI <= 23)为上面提到的开始时刻。也就是说,如果第I个申请者被录取,他(她)将从tI 时刻开始连续工作8小时。
你将编写一个程序,输入R(I)(I = 0..23)和tI (I = 1..N),它们都是非负整数,计算为满足上述限制需要雇佣的最少出纳员数目。在每一时刻可以有比对应的R(I)更多的出纳员在工作。
输入
第一行为24个整数表示R(0),R(1),…, R(23)(R(I)<= 1000)。
接下来一行是N,表示申请者数目(0 <= N <= 1000),接下来每行包含一个整数tI (0 <= tI <= 23)。
输出
输出2行,第一行包含一个整数,表示需要出纳员的最少数目;
第二行为一种最少出纳员的可行方案,即24个整数,表示每个时间点分别雇佣多少人。
样例输入
0 1 2 1 2 1 1 1 2 2 0 2 2 2 2 2 2 2 0 1 0 0 2 2
16
17
21
0
7
2
11
10
1
3
16
14
6
9
1
16
16
样例输出
6
0 0 1 0 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 0
提示
保证有解,n在10个点的数据范围:5, 10, 20, 30, 50, 100, 300, 500, 800, 1000, 1000
解题思路
除了暴力枚举以外,还可以用差分约束系统来解决。s[i]表示前面i个时间点聘用人数之和。为了避免出现负数,时间点全部加1,时间i表示i-1点到i点工作。预处理出各个时间点需要的人数放到a[i],各个时间点应聘的人数放到c[i],那么可以建立一下差分约束不等式:
1、第i个时间点聘用的人数是s[i]-s[i-1],聘用人数在0到c[i]之间,即s[i]-s[i-1]>=0 && s[i]-s[i-1]<=c[i]。
2、第i个时间点需要的人数是a[i],那么最近8个小时聘用的人数之和至少a[i]个,即s[i]-s[i-8]>=a[i];需要注意的是,当i=8时,s[i]表示前8个小时聘用人数,比s[0]多至少a[i]是没问题的,但1到7减8就会出现负数,需要特殊处理一下。我们就看s[7]吧:s[7]的前8个小时是24、1、2、3、4、5、6、7,这8个小时怎么表示?s[24] – s[23] + s[7],也就是说当i<8时,s[24]-s[i+16]+s[i]>=a[i]。这样的话,就会出现3个未知量了!如果s[24]已知,那不就没问题了吗。因此,我们可以试着猜聘用的人数ans,则表达式就变成s[i]>=s[i+16]+a[i]-ans。
3、既然我们认定聘用的总人数是ans,那么s[24]就等于ans,即s[24]-s[0]>=ans && s[24]-s[0]<=ans。
约束条件确定后,全部转成大于等于号求最长路即可。
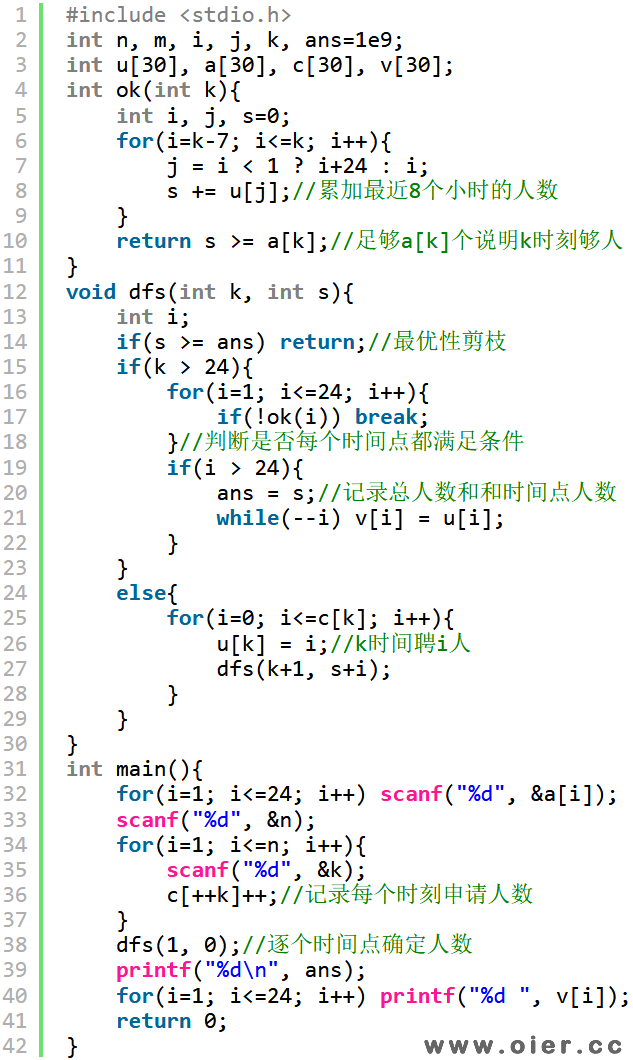
程序实现