题目大意:给定n株排成一排的花的高度,要求移走一部分,使得奇数号的话都比偶数号的花都高或者都矮,最多保留多少花?
题目描述
花匠栋栋种了一排花,每株花都有自己的高度。花儿越长越大,也越来越挤。栋栋决定把这排中的一部分花移走,将剩下的留在原地,使得剩下的花能有空间长大,同时,栋栋希望剩下的花排列得比较别致。
具体而言,栋栋的花的高度可以看成一列整数h1, h2, … , hn。设当一部分花被移走后,剩下的花的高度依次为g1, g2, … , gm,则栋栋希望下面两个条件中至少有一个满足:
条件 A:对于所有的1<i<m/2,g2i > g2i-1,且g2i > g2i+1;
条件 B:对于所有的1<i<m/2,g2i < g2i-1,且g2i < g2i+1。
注意上面两个条件在m = 1时同时满足,当m > 1时最多有一个能满足。
请问,栋栋最多能将多少株花留在原地。
输入
输入的第一行包含一个整数 n,表示开始时花的株数。
第二行包含 n 个整数,依次为h1, h2,… , hn,表示每株花的高度。
输出
输出一行,包含一个整数 m,表示最多能留在原地的花的株数。
样例输入
5
5 3 2 1 2
样例输出
3
提示
对于 20%的数据,n ≤ 10;
对于 30%的数据,n ≤ 25;
对于 70%的数据,n ≤ 1000,0 ≤ hi ≤ 1000;
对于 100%的数据,1 ≤ n ≤ 1000000,1 ≤ hi ≤ 1000000,所有的 hi 随机生成,所有随机数服从某区间内的均匀分布。
NOIP2013提高组第二天第二题
解题思路
最终剩下的,是高矮相间的波浪形的花。在波峰上,选择尽可能高的花,这对于当前的上升没有影响,对于后面选择下降的花更加有利;同样地,在波谷上,选取尽可能矮的花,对于当前的下降没有影响,对于后续选择上升的花更加有利。这样贪心的选择,实际上就是寻找拐点,有多少个拐点,就保留多少株花。如果出现方向不一样,原来是上升的突然变成下降,或者下降转为上升,就是出现拐点了,此时找个变量++,统计拐点个数即可。需要注意的是,初始方向要跟前面两个点的方向取反,因为前面两个点一定能组成符合要求的序列(在去除相邻重复的数据后——相邻高度相同的花,只能选其中的一株),总之,一定要让第二株花选到。
程序实现

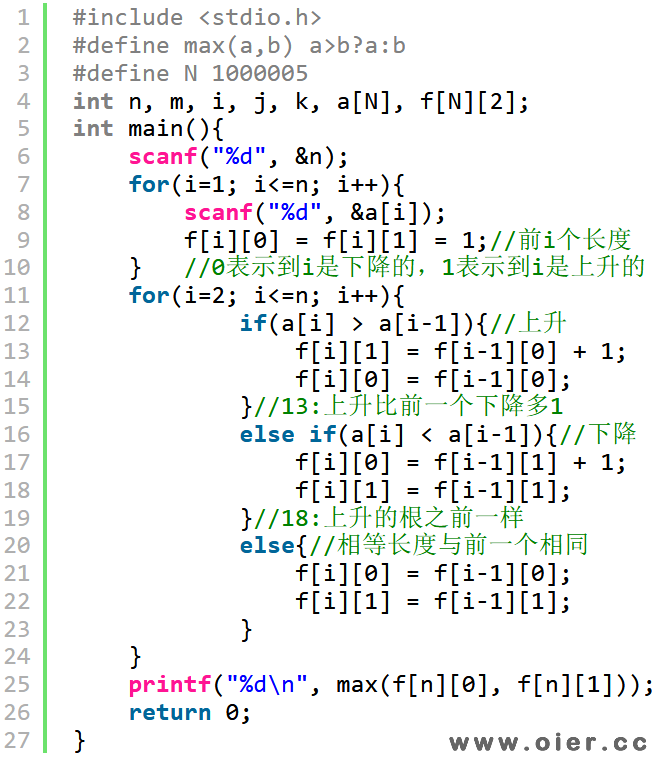
降维:一开始方向为0,与上升下降都不相同,故无论第二株花是上升还是下降,都会被选到。

80分的暴力DP:按照最长上升子序列的思想来做,f[i]表示以i结尾的最长序列,由于需要高矮相间,需要记录前一个状态的方向(上升还是下降),故开f[i][0/1],0表示下降,1表示上升。如果a[i]>a[j],那么最后是上升的,以j结尾必须是下降才能使得长度+1。最后比较f[n][0]和f[n][1]即可,因为最长的序列,肯定可以包含最后一株花——如果最后一株花是连续上升的最高点或者连续下降的最低点,那么这个单调序列中的花都可以选作为最后一株花,否则由上升转为下降或者下降转为上升,都可以多选一株花。
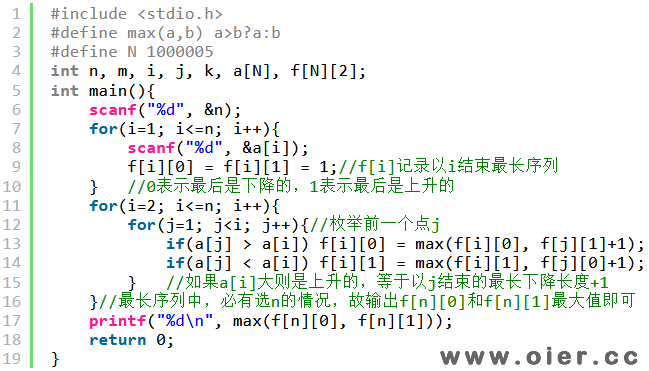
不难发现,上面的DP,复杂度是O(n^2)的,如何优化呢?外重循环是不可能的,只能优化里面的循环。为了避免遍历前面的花,我们可以改变状态的定义——f[i]表示前i株花的最长长度,0还是代表下降,1还是代表上升。这样子,如果a[i]>a[i-1],最后是上升的:f[i][0] = f[i-1][0],因为这株花都是比前面的高,在下降方向可以看成等价的;f[i][1] = f[i-1][0] + 1,即等于前一个下降的长度+1,当然f[i][1] = f[i][1]也是允许的,因为在上升方向都是越来越高,也可以看成是等价的。为什么不用写成f[i][1] = max(f[i-1][1], f[i-1][0]+1)呢?因为f[i-1][0] + 1不会比f[i-1][1]小(f[i][0]和f[i][1]最多相差1)。