SSOJ1219拦截导弹
2700+
作者：crxis 发布：2017-10-26 分类：序列DP
题目大意：导弹系统拦截导弹后，之后拦截的高度不能高于前一个的高度，先知道各个导弹依次飞来的高度，最多拦截多少个？至少还需要多少套系统？
题目描述
某国为了防御敌国的导弹袭击，研发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试验阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
输入
输入数据只有一行，该行包含若干个数据，之间用半角逗号隔开，表示导弹依次飞来的高度（导弹最多有 20 枚，其高度为不大于 30000 的正整数）。
输出
输出数据只有一行，该行包含两个数据，之间用半角逗号隔开。第一个数据表示这套系统最多能拦截的导弹数；第二个数据表示若要拦截所有导弹至少要再添加多少套这样的系统。
样例输入
389,207,155,300,299,170,158,65
样例输出
6,1
提示
注意审题，切勿直接提交过去的程序！
NOIP1999提高组第一题
解题思路
最多拦截多少个导弹，只要高度不上升就行，即求最长不上升子序列；需要多少套系统，其实是求最长上升子序列，为什么呢？如果遇到一个上升子序列，那么至少需要序列长度套系统，因为这个序列中的导弹都需要一套系统来拦截；为什么不需要更多的系统呢？因为序列中的第一个导弹前面的都不比他低（有低会更长），而且不递增（有递增选他做最长上升子序列），同样的，第一个和第二个之间的导弹也是如此，且不存在递增的2个导弹比第二个低，这样我们可以用一套系统拦截序列中的第一个导弹以及他前面的所有导弹（不递增），还有第二个之前比他低的所有导弹（不递增），由于第一个和第二个导弹间没有中间高度的导弹，拦截后最长上升子序列长度减1，只需要继续这样操作，就可以把导弹拦截完。
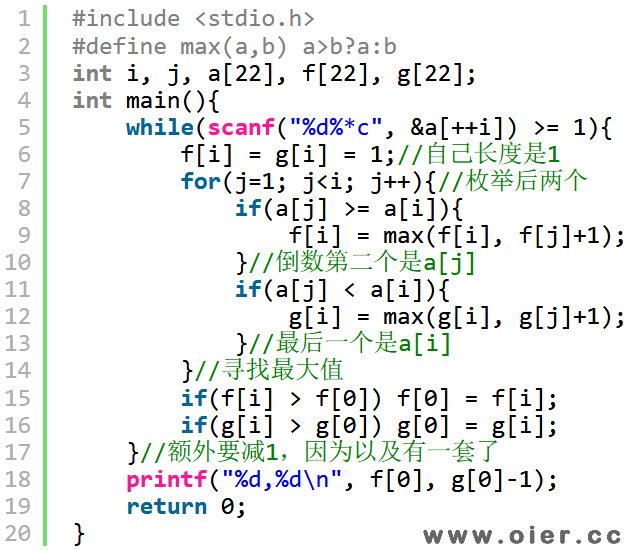
程序实现
