题目大意:给定一个函数以及某个零点存在的区间,求出该零点的位置。
题目描述
有函数:f(x) = x5 – 15 * x4+ 85 * x3– 225 * x2+ 274 * x – 121
已知 f(1.5) > 0 , f(2.4) < 0 且方程 f(x) = 0 在区间 [1.5,2.4] 有且只有一个根,请用二分法求出该根。
输入
输出
样例输入
无
样例输出
不提供
解题思路
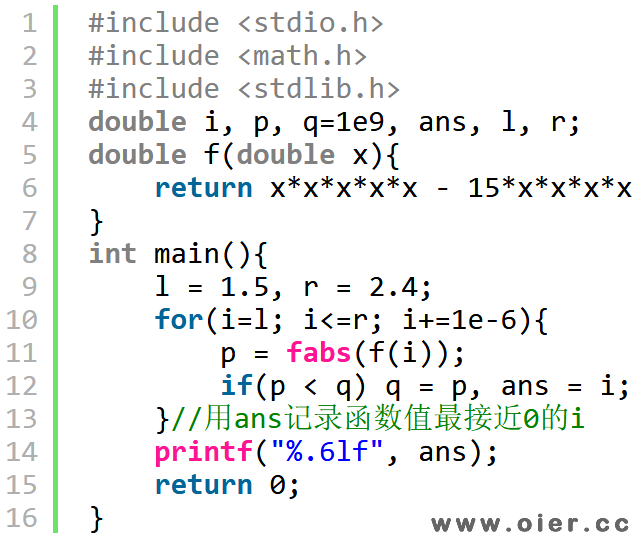
出现小数,可以转成整数去做,也可以非常小心地处理小数。区间是[1.5,2.4] ,保留6位小数,也就是从不超过100万的小数中找零点。由于是小数,不能直接判断函数值是否等于0,只能比较函数值到0的距离,越小越好。我们可以枚举这100万个小数,找到函数值最接近0的那个自变量的值,输出它即答案。
一种更快的方法是用二分。不难看成这个区间内,零点左边都大于0,右边都小于0。我们可以先猜一下中间那个小数,如果他大于0,那么区间有l-r就可以减半到m到r,否则减半到l到m,这样区间每次少一半,时间复杂度就是log级别的。那么,什么时候结束呢?区间会不存在吗?实际上,区间有可能一直变小,或者停在某个区间,因为小数是有精度问题的。因此,我们只需要让区间不大于一个很小的数,就可以当这个区间只有一个数了。题目要求保留6为小数,那么我们可以让这个区间小于1e-8,这样l和r的前面7为小数就很有可能相等,这样就比较保险。
程序实现