题目大意:两个人打牌,如果对方不出牌自己就可以得分,怎样打才能分数最多?
题目描述
凡是一个具有领导力的孩子。现实生活中他特别喜欢玩一个叫做 UNO 的纸牌游戏,他也总是带着其他小朋友一起玩,然后战胜他们。慢慢地,他厌倦了胜利,于是准备发明一种新的双人纸牌游戏。
初始时,每个人手中都有若干张牌(也可能没有),然后由凡开始轮流出牌,当轮到自己出牌的时候,可以选择:
- 出一张牌使得待定分数加 1。
- 不出牌,对方的得分加上现在的待定分数,然后待定分数变为 0。
无论选择什么,接下来都轮到对手出牌。
为了能让这个游戏进行下去,假如现在的待定分数为 0,当前出牌的人就不能选择不出牌,除非他没有手牌了。
当然作为一个竞技类纸牌游戏,你的得分减去对手的得分自然越高越好。
凡依旧在不断的赢啊赢,直到一个带着面具的邻家男孩出现,成为了他旗鼓相当的对手,慢慢地,凡觉得自己玩不过那个男孩了,因为他总是会使用最优策略……于是他来向你求助,希望你也能帮他使用最优策略!
输入
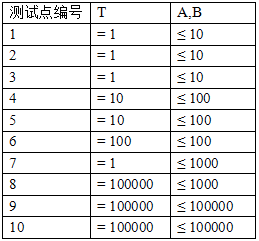
第一行一个正整数 T,代表凡向你求助的次数。
接下来 T 行,每行两个非负整数 A,B。A 代表凡的手牌数量,B 代表邻家男孩的手牌数量。
输出
对于每次求助,输出每行一个整数,表示在双方都使用最优策略情况下,凡的得分减去邻家男孩得分的值。
样例输入
1
4 1
样例输出
1
提示
样例解释
凡先打出一张牌,对方不出牌,手牌数为 3,1,得分为 1,0。
凡再打出一张牌,对方不出牌,手牌数为 2,1,得分为 2,0。
凡接着打出一张牌,对方不出牌,手牌数为 1,1,得分为 3,0。
凡只能再打出一张牌,对方出牌,手牌数为 0,0,得分为 3,2。
可以证明双方都没有更好的策略
解题思路
问题可以简化成A和B打牌,双方都适用最优策略,A先出牌,如果B一直不出牌,直到A出完最后一张牌才开始出牌,那么A得分为a-1,B得分为b+1,也就是说B至少能够得b+1分,A至多得a-1分。反之,如果B在某一时刻出牌了,A要么继续出牌,要么不出牌:如果A等到B出完最后一张牌才出牌,那么B只能得到b分,A能够得到a分;如果A中途出牌了,那么B同样至多拿b+1分。因此,对于B来说,只要不出牌,就能够得到最多的分数,最终得分必是A的得分为a-1,B的得分为b-1。最后考虑一下牌为0的特殊情况即可。
程序实现