题目大意:已知投注,且无论如何赔的钱比赚的钱要多,如何设置返还金额,才能使赔的前最少?
题目描述
凡和邻家男孩玩完了纸牌,兴致很高,于是准备了一场表演艺术对抗赛。 他特意请来了很多表演艺术家,分成绿黑两队,进行名为 PK,实则捞金的表演。
凡为了捞金,开设了一个赌局,在比赛开始之前招揽人们来押注谁能胜出,在所有人进行投注之后,凡需要告诉大家绿方和黑方的单位返还金额都是多少。
举个例子,如果绿方的单位返还金额为 5,那么我每押 1 块钱绿方胜,如果成真就能拿回 5 块钱,但是如果结果绿方输了,我就拿不回来任何钱。
凡决定将单位返还金额设得更具有吸引力,所以他要求“绿方胜的单位返还金额+黑方胜的单位返还金额=T”,并且为了赚更多的钱,凡可以在中间某两个投注的人之间更改单位返还金额,但是要求双方的总和仍然为 T,并且只能更改一次。
不幸的是,凡突然发现自己请来的表演艺术家竟然和众多投注人是一伙的,也就是说,在凡定下单位返还金额之后,那些艺术家会操纵比赛结果,从而让凡拿出更多的钱来。
这下凡有些慌了,于是他来询问你应该怎么制定单位返还金额。
输入
第一行一个整数 N(1≤N≤5∗105),代表投注的人的个数。
接下来 N 行,每行两个实数 ai,bi(1≤ai,bi≤100) 代表第 i 个人投注黑方胜和绿方胜的资金。
最后一行一个实数 T(1≤T≤100),含义如题目中所示。
输出
一个实数,代表你最少返还的金额(保留两位小数)。
样例输入
样例输入1
3
0 10
10 0
10 0
10
样例输入2
2
5 5
5 5
1
样例输出
样例输出1
0.00
样例输出2
5.00
提示
样例解释 1
一种最优方案是:
第一次投注及之前,单位返还金额为 10 和 0。
第二次投注及之后,单位返还金额为 0 和 10
这样无论哪方胜利,你都不会返还任何金钱。
样例解释 2
一种最优方案是:
第一次投注及之前,单位返还金额为 0.5 和 0.5。
第二次投注及之后,单位返还金额为 0.5 和 0.5
这样无论哪方胜利,你的返还金额都为 5。
解题思路
不管如何设置返还金额,如果出现一方比另一方多,那么赔的肯定是多的那一方,因为表演艺术家和投注人是一伙的!因此,投注双方赢/赔的钱要一样多!
设置半部分返还金额是p,后半部分返还金额是q,前半部分绿和黑分别投注为a和c,后半部分分别为b和d,那么p*a+q*c = (t-p)*b + (t-q)*d,即p*(a+b) + q*(c+d) = t*(b+d)。现在要返还的钱最少,也就是在满足上述等式的情况下(双方一样多),使a*p+c*q最少。不难发现,p和q成反比例,如果a>c,那么p越大越好,所以p取最大值有可能出现最好;有p减小,q增大,有可能q增大速度更快,出现更好情况,因此,q去最大值也可能出现最优值。在两个最值中选一个,就能找到最优答案。
如何找最值?p=0,q即最大,但q有可能超过t;同理,q=0,p最大,不能让他超过t。
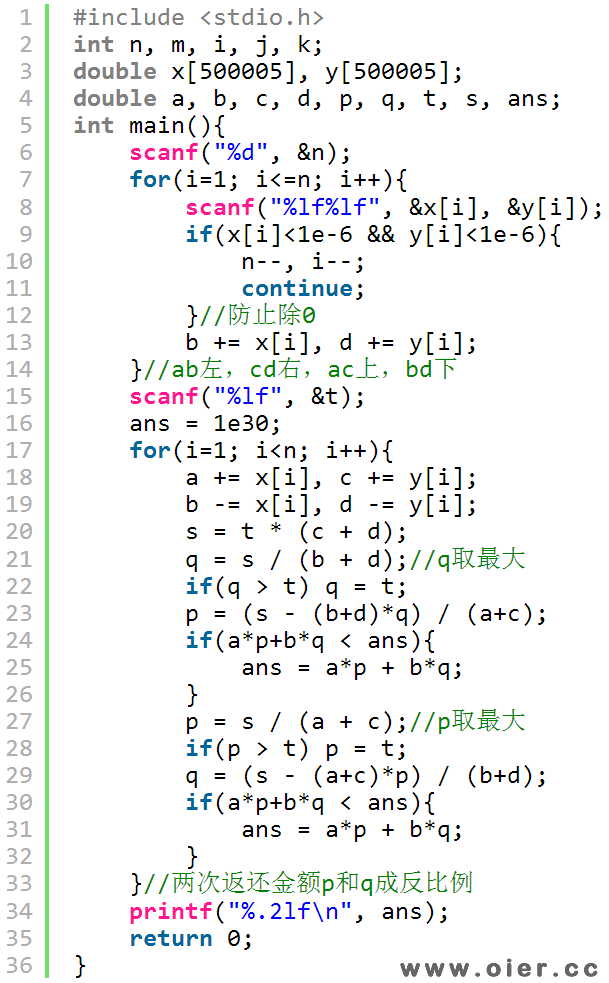
程序实现