题目大意:从根节点开始种树,每天只能选一个与树相邻的结点种树,每个结点的生长规律跟abc有关,请问最早什么时候所有树都达到指定高度?
题目描述
你是一个森林养护员,有一天,你接到了一个任务:在一片森林内的地块上种树,并养护至树木长到指定的高度。
森林的地图有 $n$ 片地块,其中 $1$ 号地块连接森林的入口。共有 $n-1$ 条道路连接这些地块,使得每片地块都能通过道路互相到达。最开始,每片地块上都没有树木。
你的目标是:在每片地块上均种植一棵树木,并使得 $i$ 号地块上的树的高度生长到不低于 $a_i$ 米。
你每天可以选择一个未种树且**与某个已种树的地块直接邻接**(**即通过单条道路相连**)的地块,种一棵高度为 $0$ 米的树。如果所有地块均已种过树,则你当天不进行任何操作。特别地,第 $1$ 天你只能在 $1$ 号空地种树。
对每个地块而言,从该地块被种下树的当天开始,该地块上的树每天都会生长一定的高度。由于气候和土壤条件不同,在第 $x$ 天,$i$ 号地块上的树会长高 $\max(b_i + x \times c_i, 1)$ 米。注意这里的 $x$ 是从整个任务的第一天,而非种下这棵树的第一天开始计算。
你想知道:最少需要多少天能够完成你的任务?
输入输出格式
输入格式
输入的第一行包含一个正整数 $n$,表示森林的地块数量。
接下来 $n$ 行:每行包含三个整数 $a_i, b_i, c_i$,分别描述一片地块,含义如题目描述中所述。
接下来 $n-1$ 行:每行包含两个正整数 $u_i, v_i$,表示一条连接地块 $u_i$ 和 $v_i$ 的道路。
输出格式
输入输出样例
输入样例 #1
4
12 1 1
2 4 -1
10 3 0
7 10 -2
1 2
1 3
3 4输出样例 #1
5
说明
**【样例 1 解释】**
第 $1$ 天:在地块 $1$ 种树,地块 $1$ 的树木长高至 $2$ 米。
第 $2$ 天:在地块 $3$ 种树,地块 $1, 3$ 的树木分别长高至 $5, 3$ 米。
第 $3$ 天:在地块 $4$ 种树,地块 $1, 3, 4$ 的树木分别长高至 $9, 6, 4$ 米。
第 $4$ 天:在地块 $2$ 种树,地块 $1, 2, 3, 4$ 的树木分别长高至 $14, 1, 9, 6$ 米。
第 $5$ 天:地块 $1, 2, 3, 4$ 的树木分别长高至 $20, 2, 12, 7$ 米。
**【样例 2】**
见选手目录下的 `tree/tree2.in` 与 `tree/tree2.ans`。
**【样例 3】**
见选手目录下的 `tree/tree3.in` 与 `tree/tree3.ans`。
**【样例 4】**
见选手目录下的 `tree/tree4.in` 与 `tree/tree4.ans`。
**【数据范围】**
对于所有测试数据有:$1 ≤ n ≤ 10^5,1 ≤ a_i ≤ 10^{18}, 1 ≤ b_i ≤ 10^9,0 ≤ |c_i| ≤ 10^9, 1 ≤ u_i, v_i ≤ n$。保证存在方案能在 $10^9$ 天内完成任务。
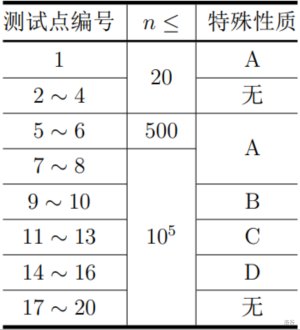
特殊性质 A:对于所有 $1 ≤ i ≤ n$,均有 $c_i = 0$;
特殊性质 B:对于所有 $1 ≤ i < n$,均有 $u_i = i$、$v_i = i + 1$;
特殊性质 C:与任何地块直接相连的道路均不超过 $2$ 条;
特殊性质 D:对于所有 $1 ≤ i < n$,均有 $u_i = 1$。
解题思路
本题难在二分,会二分骗取暴力分,基本上就可以想到正解,二分套二分不比贪心难,却能让很多选手不敢做下去。
首先,答案可以二分,时间m可以,m+1肯定也可以;时间m不行,m-1也不行。确定结束时间后,种树时间也更好确定了。
其次,二分求每个点最晚种树时间,范围是[0, n],0表示无解,n已是最后一天,不需要再多。
坑点在于求一段时间内树的高度:如果c非负,那么b只需要乘以天数,c则需要乘以要给等差数列的和,三个数乘起来可能爆long long。
解决方法:相乘会爆,那就用除法验证。三个数乘起来超过5e18肯定满足高度要求,之间返回无穷大,否则直接算也不会超过6e18。
愚蠢做法:用__int128,需要慢慢卡常吧?
最后,就是后序遍历这棵树,让父亲结点比儿子结点早一天,按照时间排序依次种树验证即可。
程序实现

(“考场代码”,感谢宋同学的“监督”;想更快,可以用树状数组、快读等优化)
原来是这样用的 😉