题目大意:一个字符串,相邻两个字母相同可以消除,请问其中有多少个子串是可以被消除的?
题目描述
个相邻的元素。现在,他有一个长度为 $n$ 且仅由小写字母构成的字符串。我们称一个字符串是可消除的,当且仅当可以对这个字符串进行若干次操作,使之成为一个空字符串。
其中每次操作可以从字符串中删除两个相邻的相同字符,操作后剩余字符串会拼接在一起。
小 L 想知道,这个字符串的所有非空连续子串中,有多少个是可消除的。
输入输出格式
输入格式
输入的第一行包含一个正整数 $n$,表示字符串的长度。
输入的第二行包含一个长度为 $n$ 且仅由小写字母构成的的字符串,表示题目中询问的字符串。
输出格式
输入输出样例
输入样例 #1
8
accabccb
输出样例 #1
5说明
**【样例 1 解释】**
一共有 $5$ 个可消除的连续子串,分别是 `cc`、`acca`、`cc`、`bccb`、`accabccb`。
**【样例 2】**
见选手目录下的 `game/game2.in` 与 `game/game2.ans`。
**【样例 3】**
见选手目录下的 `game/game3.in` 与 `game/game3.ans`。
**【样例 4】**
见选手目录下的 `game/game4.in` 与 `game/game4.ans`。
**【数据范围】**
对于所有测试数据有:$1 \le n \le 2 \times 10^6$,且询问的字符串仅由小写字母构成。
| 测试点 | $n\leq$ | 特殊性质 |
| :———-: | :———-: | :———-: |
| $1\sim 5$ | $10$ | 无 |
| $6\sim 7$ | $800$ | 无 |
| $8\sim 10$ | $8000$ | 无 |
| $11\sim 12$ | $2\times 10^5$ | A |
| $13\sim 14$ | $2\times 10^5$ | B |
| $15\sim 17$ | $2\times 10^5$ | 无 |
| $18\sim 20$ | $2\times 10^6$ | 无 |
特殊性质 A:字符串中的每个字符独立等概率地从字符集中选择。
特殊性质 B:字符串仅由 `a` 和 `b` 构成。
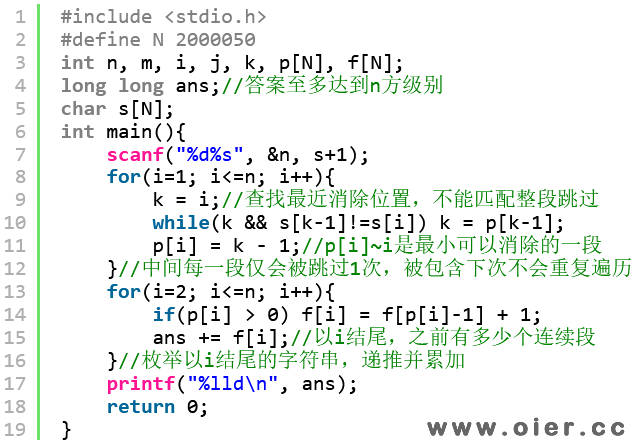
解题思路
50分做法:8000的平方不超时,枚举字符串开头,依次遍历到结尾,用栈维护当前子串是否能被全部消除,如果可以则增加一种方案。

满分做法:找规律,发现对于同一个开头,可以完全消除,那么这个字串要么是最近匹配,要么是多个消除字串拼接而成,可以用“前缀和”的思想,递推出以i结尾的字符串方案。
1、如果维护以i结尾最近匹配位置p[i]?当前位置位i,之前匹配位置为p[i],那么p[i]+1~i-1都是匹配的,也就是说p[i-1] = p[i]+1,如果不行继续往前找就行。这样不会超时,因为每一个字符只会被遍历一次,如果这次遍历了,那么下次会直接被包含到一个消除子串,可以直接跳过。
2、递推与求和:以i结尾,首先得到子串p[i]~i,如果之前以p[i]-1结尾存在方案,可以直接接过来,累加即可。
程序实现
原来是这样用的 😉