题目大意:已知n、e、d、p<q,以及$n = p \times q$、$e \times d = (p – 1)(q – 1) + 1$,求p和q,无解输出NO。
题目描述
输入输出格式
输入格式
第一行一个正整数 $k$,表示有 $k$ 次询问。
接下来 $k$ 行,第 $i$ 行三个正整数 $n_i, d_i, e_i$。
输出格式
输出 $k$ 行,每行两个正整数 $p_i, q_i$ 表示答案。
为使输出统一,你应当保证 $p_i \leq q_i$。
如果无解,请输出 `NO`。
输入输出样例
输入样例 #1
10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109
输出样例 #1
2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88
说明
**【样例 \#2】**
见附件中的 `decode/decode2.in` 与 `decode/decode2.ans`。
**【样例 \#3】**
见附件中的 `decode/decode3.in` 与 `decode/decode3.ans`。
**【样例 \#4】**
见附件中的 `decode/decode4.in` 与 `decode/decode4.ans`。
**【数据范围】**
以下记 $m = n – e \times d + 2$。
保证对于 $100\%$ 的数据,$1 \leq k \leq {10}^5$,对于任意的 $1 \leq i \leq k$,$1 \leq n_i \leq {10}^{18}$,$1 \leq e_i \times d_i \leq {10}^{18}$
,$1 \leq m \leq {10}^9$。
| 测试点编号 | $k \leq$ | $n \leq$ | $m \leq$ | 特殊性质 |
| :———-: | :———-: | :———-: | :———-: | :———-: |
| $1$ | $10^3$ | $10^3$ | $10^3$ | 保证有解 |
| $2$ | $10^3$ | $10^3$ | $10^3$ | 无 |
| $3$ | $10^3$ | $10^9$ | $6\times 10^4$ | 保证有解 |
| $4$ | $10^3$ | $10^9$ | $6\times 10^4$ | 无 |
| $5$ | $10^3$ | $10^9$ | $10^9$ | 保证有解 |
| $6$ | $10^3$ | $10^9$ | $10^9$ | 无 |
| $7$ | $10^5$ | $10^{18}$ | $10^9$ | 保证若有解则 $p=q$ |
| $8$ | $10^5$ | $10^{18}$ | $10^9$ | 保证有解 |
| $9$ | $10^5$ | $10^{18}$ | $10^9$ | 无 |
| $10$ | $10^5$ | $10^{18}$ | $10^9$ | 无 |
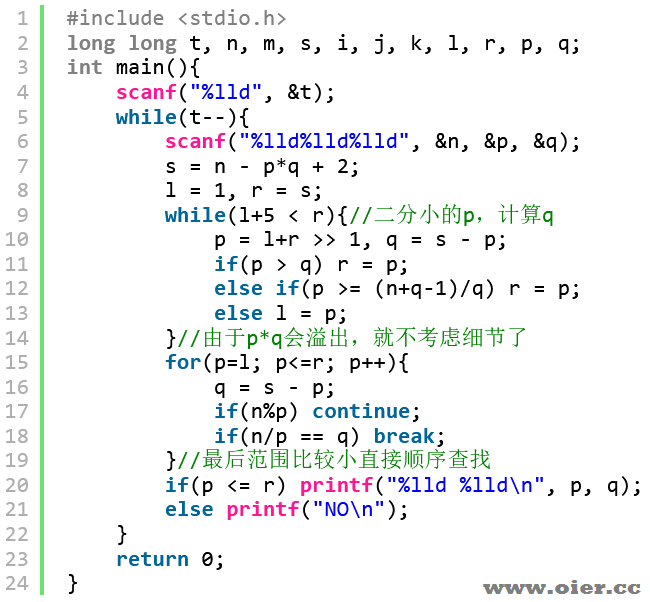
解题思路
化简可得p+q = n-e*d+2,也就是最终可以得到p*q = n、p+q = m的两个式子,暴力枚举会超时,可以考虑二分答案。
周长相同,正方形面积最大,也就是说p和q越接近,n就越大。我们可以二分p,计算q,如果p*q太大,那么p要小一点(跟q拉开距离),否则p要大一点(拉近距离)。
由于p*q会超出long long范围,除法有精度,特判比较麻烦,我们可以二分得到一个较小范围后,再暴力枚举即可。
程序实现
原来是这样用的 😉