题目大意:已知$z=x\times y\times\gcd(x,y)$,给出x和z,求最小的满足要求的y,无解输出-1。
题目描述
Kri 喜欢玩数字游戏。
一天,他在草稿纸上写下了 $t$ 对正整数 $(x,y)$,并对于每一对正整数计算出了 $z=x\times y\times\gcd(x,y)$。
可是调皮的 Zay 找到了 Kri 的草稿纸,并把每一组的 $y$ 都擦除了,还可能改动了一些 $z$。
现在 Kri 想请你帮忙还原每一组的 $y$,具体地,对于每一组中的 $x$ 和 $z$,你需要输出最小的正整数 $y$,使得 $z=x\times y\times\gcd(x,y)$。如果这样的 $y$ 不存在,也就是 Zay 一定改动了 $z$,那么请输出 $-1$。
注:$\gcd(x,y)$ 表示 $x$ 和 $y$ 的最大公约数,也就是最大的正整数 $d$,满足 $d$ 既是 $x$ 的约数,又是 $y$ 的约数。
输入输出格式
输入格式
第一行一个整数 ,表示有 $t$ 对正整数 $x$ 和 $z$。
接下来 $t$ 行,每行两个正整数 $x$ 和 $z$,含义见题目描述。
输出格式
输入输出样例
输入样例 #1
1
10 240输出样例 #1
12输入样例 #2
3
5 30
4 8
11 11输出样例 #2
6
-1
1输入样例 #3
见附件中的 math3.in输出样例 #3
见附件中的 math3.out输入样例 #4
见附件中的 math4.in输出样例 #4
见附件中的 math4.out说明
**【样例 1 解释】**
$x\times y\times \gcd(x,y)=10\times 12\times\gcd(10,12)=240$。
**【数据范围】**
对于 $20\%$ 的数据,$t, x, z \le {10}^3$。
对于 $40\%$ 的数据,$t \le {10}^3$,$x \le {10}^6$,$z \le {10}^9$。
对于另 $30\%$ 的数据,$t \le {10}^4$。
对于另 $20\%$ 的数据,$x \le {10}^6$。
对于 $100\%$ 的数据,$1 \le t \le 5 \times {10}^5$,$1 \le x \le {10}^9$,$1 \le z < 2^{63}$。
解题思路
设x和y的最大公约数gcd(x, y)为d,x = pd,y = qd,z = pqddd。
z/x = qdd,关键在于d取多少?
不难发现,p、q互质,但x和z/x的最大公约数不一定为d,因为p和d不一定互质,q和d也不一定互质。
想办法把d的影响去掉,看$x^2$和z/d,即ppdd和qdd,他们的最大公约数显然是dd,求出dd即可得到d,从而得到y。
最后代入验证是否满足条件即可。
程序实现
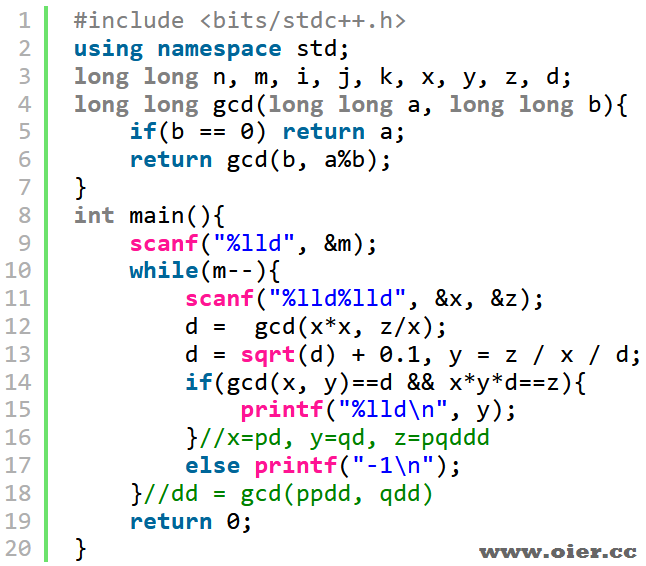
暴力满分代码:
1、枚举优化:想办法缩小枚举范围
2、约数是成对存在的

原来是这样用的 😉