洛谷P8252讨论[NOI Online 2022]
1442+
作者：crxis 发布：2022-03-27 分类：贪心
题目大意：n个人n到题目，每个人会若干道题目，两个人会讨论，当且仅当有题目大家都会，且各自会另一个人不会的题目，输出会讨论的两人，或者无解。
题目描述
有 $n$ 个人正在打模拟赛，模拟赛有 $n$ 道题目。
有两人都会的题目并且没有人会的题目包含另一个人时，两者之间才会讨论。
（定义第 $i$ 个人会的题目的集合为 $S_i$ ，即当 $S_x\cap S_y\neq\varnothing\land S_x\not\subseteq S_y\land S_y\not\subseteq S_x$ 时，第 $x$ 人和第 $y$ 人会讨论）
为了让模拟赛的效果更好，希望你可以找出一对会讨论的人或判断不存在。
有两人都会的题目并且没有人会的题目包含另一个人时，两者之间才会讨论。
（定义第 $i$ 个人会的题目的集合为 $S_i$ ，即当 $S_x\cap S_y\neq\varnothing\land S_x\not\subseteq S_y\land S_y\not\subseteq S_x$ 时，第 $x$ 人和第 $y$ 人会讨论）
为了让模拟赛的效果更好，希望你可以找出一对会讨论的人或判断不存在。
输入输出格式
输入格式
第一行一个正整数 $T$ 表示数据组数，对于每组数据：
第一行一个正整数 $n$ 表示人数和题目数量。
接下来 $n$ 行，第 $i$ 行第一个自然数 $k_i$ 表示第 $i$ 个人会 $k_i$ 道题。接下来 $k_i$ 个正整数，每个数 $x$ 表示第 $i$ 个人会第 $x$ 道题。
第一行一个正整数 $n$ 表示人数和题目数量。
接下来 $n$ 行，第 $i$ 行第一个自然数 $k_i$ 表示第 $i$ 个人会 $k_i$ 道题。接下来 $k_i$ 个正整数，每个数 $x$ 表示第 $i$ 个人会第 $x$ 道题。
输出格式
对于每组数据：
如果没有会讨论的人，输出 `NO`。
否则第一行输出 `YES`，第二行输出两个正整数 $x$ 和 $y$，表示第 $x$ 人和第 $y$ 人会讨论。
如果有多种方案，输出任意一种即可。
如果没有会讨论的人，输出 `NO`。
否则第一行输出 `YES`，第二行输出两个正整数 $x$ 和 $y$，表示第 $x$ 人和第 $y$ 人会讨论。
如果有多种方案，输出任意一种即可。
输入输出样例
输入样例 #1
2
5
4 1 2 3 5
3 1 2 3
2 1 2
1 1
1 4
4
3 1 2 3
3 2 3 4
0
4 1 2 3 4输出样例 #1
NO
YES
1 2说明
**【样例 2】**
见附件中的 `discuss/discuss2.in` 与 `discuss/discuss2.ans`。
**【数据范围与提示】**
对于所有测试点：令一组数据中 $m=\sum k_i$，则 $1\le T\le 5$，$1\le \sum n\le {10}^6$，$1\le m\le 2\times {10}^6$，$0\le k_i\le n$。
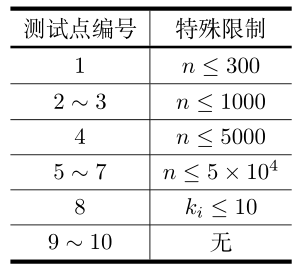
每个测试点的具体限制见下表：
解题思路
参与讨论的2个人，首先有共同题目，其次会另一个人不会的题目。
我们可以按照会做题数量从大到小排序，这样只要有共同题目，就只需要满足下一个人有新的题目。
为什么，因为下一个人有新题，之前的人题量不比他少，必然各自有自己的题目。
如何判断当前的人有新题？依次标记每道题属于谁（题量少的覆盖题量大的，但覆盖不满），如果不属于任何人，就是有新题；如果不同题目分别属于不同的人（至少与2人重叠），那么相对于题量少的那个，当前的人也是有新题的，可以跟题量少的那个讨论。因为题量少的那个，必然不会另一道重叠的题（题量大的反而可能包含当前的人）。
这样，记录跟谁有共同题目，只要还满足有新题，即可找到一组答案：一个是自己，一个是另一个有共同题目的人（两人选题量少的那个）。
程序实现
原来是这样用的 😉