题目大意:一个长度为n的不下降序列,可以将 $a_i$ 变为 $a_{i – 1} + a_{i + 1} – a_i$,请问方差最小可以是多少?输出方差乘以n的平方。
题目描述
给定长度为 $n$ 的非严格递增正整数数列 $1 \le a_1 \le a_2 \le \cdots \le a_n$。每次可以进行的操作是:任意选择一个正整数 $1 < i < n$,将 $a_i$ 变为 $a_{i – 1} + a_{i + 1} – a_i$。求在若干次操作之后,该数列的方差最小值是多少。请输出最小值乘以 $n^2$ 的结果。
其中方差的定义为:数列中每个数与平均值的差的平方的平均值。更形式化地说,方差的定义为 $D = \frac{1}{n} \sum_{i = 1}^{n} {(a_i – \bar a)}^2$,其中 $\bar a = \frac{1}{n} \sum_{i = 1}^{n} a_i$。
输入输出格式
输入格式
输入的第一行包含一个正整数 $n$,保证 $n \le {10}^4$。
输入的第二行有 $n$ 个正整数,其中第 $i$ 个数字表示 $a_i$ 的值。数据保证 $1 \le a_1 \le a_2 \le \cdots \le a_n$。
输出格式
输入输出样例
输入样例 #1
4
1 2 4 6
输出样例 #1
52
输入样例 #2
见附件中的 variance/variance2.in输出样例 #2
见附件中的 variance/variance2.ans输入样例 #3
见附件中的 variance/variance3.in输出样例 #3
见附件中的 variance/variance3.ans输入样例 #4
见附件中的 variance/variance4.in输出样例 #4
见附件中的 variance/variance4.ans说明
**【样例解释 #1】**
对于 $(a_1, a_2, a_3, a_4) = (1, 2, 4, 6)$,第一次操作得到的数列有 $(1, 3, 4, 6)$,第二次操作得到的新的数列有 $(1, 3, 5, 6)$。之后无法得到新的数列。
对于 $(a_1, a_2, a_3, a_4) = (1, 2, 4, 6)$,平均值为 $\frac{13}{4}$,方差为 $\frac{1}{4}({(1 – \frac{13}{4})}^2 + {(2 – \frac{13}{4})}^2 + {(4 – \frac{13}{4})}^2 + {(6 – \frac{13}{4})}^2) = \frac{59}{16}$。
对于 $(a_1, a_2, a_3, a_4) = (1, 3, 4, 6)$,平均值为 $\frac{7}{2}$,方差为 $\frac{1}{4} ({(1 – \frac{7}{2})}^2 + {(3 – \frac{7}{2})}^2 + {(4 – \frac{7}{2})}^2 + {(6 – \frac{7}{2})}^2) = \frac{13}{4}$。
对于 $(a_1, a_2, a_3, a_4) = (1, 3, 5, 6)$,平均值为 $\frac{15}{4}$,方差为 $\frac{1}{4} ({(1 – \frac{15}{4})}^2 + {(3 – \frac{15}{4})}^2 + {(5 – \frac{15}{4})}^2 + {(6 – \frac{15}{4})}^2) = \frac{59}{16}$。
**【数据范围】**
| 测试点编号 | $n \le$ | $a_i \le$ |
|:-:|:-:|:-:|
| $1 \sim 3$ | $4$ | $10$ |
| $4 \sim 5$ | $10$ | $40$ |
| $6 \sim 8$ | $15$ | $20$ |
| $9 \sim 12$ | $20$ | $300$ |
| $13 \sim 15$ | $50$ | $70$ |
| $16 \sim 18$ | $100$ | $40$ |
| $19 \sim 22$ | $400$ | $600$ |
| $23 \sim 25$ | ${10}^4$ | $50$ |
对于所有的数据,保证 $1 \le n \le {10}^4$,$1 \le a_i \le 600$。
解题思路
n=4,打表找规律。
随便整4个数,如1 2 7 9,那么可以衍生出:
1 6 7 9、1 6 8 9、1 3 8 9、1 3 4 9、1 2 4 9、1 2 7 9……
他们相邻两项的差分别是:5 1 2、5 2 1、2 5 1、2 1 5、1 2 5、1 5 2……
无论怎么编号,相邻两项的差值组成的集合是一样的。
爆搜$a_i$是否改变,很难结束,能不能尝试爆搜差值呢?
爆搜差值的排列,可得20分,贪心一下,可得48分!
方差公式推导:s为$a_i$之和$\sum{a_i}$,c为$a_i$的平方和$\sum{a_i^2}$,a为平均值$\frac{s}{n}$。
$n*\sum{(a_i – a)^2} = n*c – 2*n*s*a + n*n*\frac{s}{n}^2 = n*c – s*s$
程序实现
对于这些差值,显然差值小的尽量接近平均值、尽量放中间,其他差值,从小到大放两边。
假设平均值为x,对于中间元素必定尽量接近平均值,所以肯定会选择差值小的,而差值的排列,对平均值“最”左边、“最”右边的值并没有影响。
基于这样的贪心,我们可以从小到大依次枚举每个差值放在最小差值的左边还是右边,最后依次递推出序列a求方差,时间复杂度$O(n*2^n)$,可得48分。
(感谢zhangtingxi提供思路)
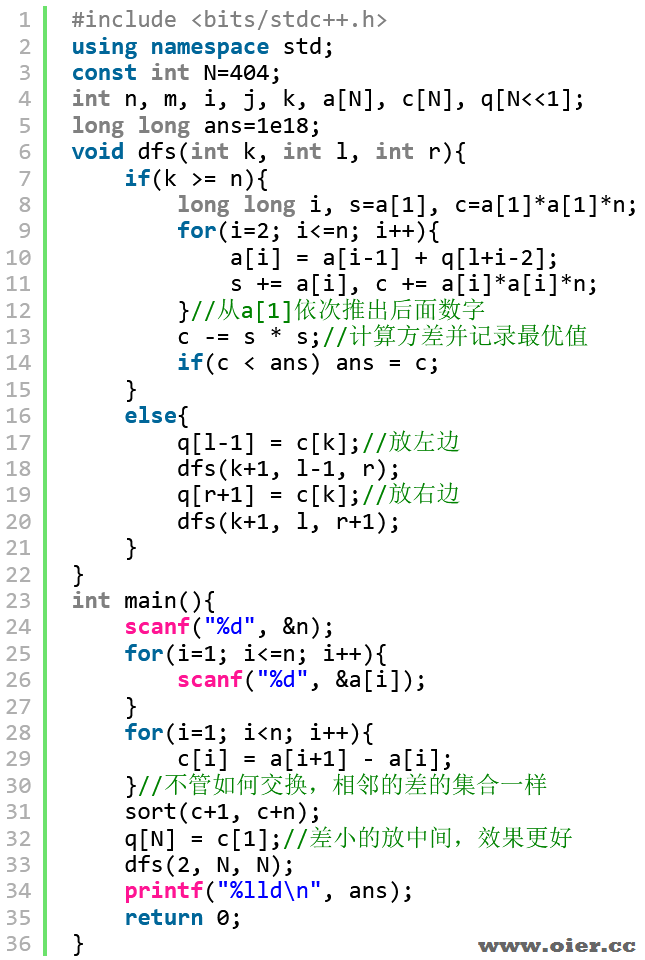
尝试把最终计算序列之和、序列平方和的部分写到爆搜中间过程,这样就可以实现剪枝或者记忆化了。
由于$a_i$还不确定,我们只能暂时记录差分序列之和与平方和。
最终左边加入$a_1$,那么后面的s和c就可以算出来:
对于和,每一项差分序列之和都需要加$a_1$,即需要加$n * a_1$。
对于平方和,原来每一项的平方,都要先增加$a_1$再平方。不妨设原来各项部分差分和分别是x、y、z,首项是a,那么$c = x^2 + y^2 + z^2$,需要变为$c = (x+a)^2 + (y+a)^2 + (z+a)^2$,只需要增加$k * a^2 + 2*a*s$。
这样,我们就可以边爆搜边处理元素之和、平方之和了。
对于72分数据,我们可以开二维数组f[105][6005]对函数参数进行记忆化:f[k][x] = y,x为各项之和,不差过$n*a_n$。
对于84分数据,我们可以直接开map,动态分配空间,从而记忆化更多的测试点。
(官方数据满分!!!)

之所以没有满分,是因为重复搜索太多。深搜记忆化超时,可以改倒搜、广搜、DP,以下是改广搜的代码:按照广度优先,我们可以控制k是一层一层搜索的,这样就可以用滚动数组,避免超空间。队列中只有两层的数据,一层至多24万种和,因为会重复入队,稍微开大一点队列,循环使用即可。
广搜代码最终没有管$a_1$,是因为y*n-x*x展开后,发现大家加的一样多,可以抵消,所以可以省略一部分代码。

=====================爆搜AC代码====================
认真思考可以发现更多性质,用于剪枝提高效率即可通过。如数字很多但数值范围很小,差分序列范围更小。假设有n个数字,数字大小不超过m,那么差分序列约√m种差值,因为差值加起来达到m了,而且有很多重复,差值为0的更多,差值不为0的不超过m个。
如何利用这些性质进行剪枝?
第一,差值为0的,放左边和放右边,效果是一样的,我们统一放左边,这样就只需要爆搜差值不为0的部分,时间复杂度由O(2n)降低到了O(2m)。
第二,对于差值c,如果有k个,他们放左边和放右边是顺序无关的,我们可以指定顺序,先放左边,再放右边,避免重复,这样每一种差值的爆搜复杂度,由O(2k)降低到了O(k)。
在爆搜基础上,加上这两个剪枝,竟然满分通过官方数据,虽然样例4超时!
