题目大意:有n个位置,x架国内飞机、y架国外飞机,已知飞机到达时间,到达后有位置就会停,否则会飞去其他地方;请问这n个位置怎么分配,才能停更多的飞机?
题目描述
当一架飞机抵达机场时,可以停靠在航站楼旁的廊桥,也可以停靠在位于机场边缘的远机位。乘客一般更期待停靠在廊桥,因为这样省去了坐摆渡车前往航站楼的周折。然而,因为廊桥的数量有限,所以这样的愿望不总是能实现。
机场分为国内区和国际区,国内航班飞机只能停靠在国内区,国际航班飞机只能停靠在国际区。一部分廊桥属于国内区,其余的廊桥属于国际区。
L 市新建了一座机场,一共有 $n$ 个廊桥。该机场决定,廊桥的使用遵循“先到先得”的原则,即每架飞机抵达后,如果相应的区(国内/国际)还有空闲的廊桥,就停靠在廊桥,否则停靠在远机位(假设远机位的数量充足)。该机场只有一条跑道,因此不存在两架飞机同时抵达的情况。
现给定未来一段时间飞机的抵达、离开时刻,请你负责将 $n$ 个廊桥分配给国内区和国际区,使停靠廊桥的飞机数量最多。
输入输出格式
输入格式
输入的第一行,包含三个正整数 $n, m_1, m_2$,分别表示廊桥的个数、国内航班飞机的数量、国际航班飞机的数量。
接下来 $m_1$ 行,是国内航班的信息,第 $i$ 行包含两个正整数 $a_{1, i}, b_{1, i}$,分别表示一架国内航班飞机的抵达、离开时刻。
接下来 $m_2$ 行,是国际航班的信息,第 $i$ 行包含两个正整数 $a_{2, i}, b_{2, i}$,分别表示一架国际航班飞机的抵达、离开时刻。
每行的多个整数由空格分隔。
输出格式
输入输出样例
输入样例 #1
3 5 4
1 5
3 8
6 10
9 14
13 18
2 11
4 15
7 17
12 16
输出样例 #1
7
输入样例 #2
2 4 6
20 30
40 50
21 22
41 42
1 19
2 18
3 4
5 6
7 8
9 10
输出样例 #2
4
输入样例 #3
见附件中的 airport/airport3.in。输出样例 #3
见附件中的 airport/airport3.ans。说明
**【样例解释 #1】**

在图中,我们用抵达、离开时刻的数对来代表一架飞机,如 $(1, 5)$ 表示时刻 $1$ 抵达、时刻 $5$ 离开的飞机;用 $\surd$ 表示该飞机停靠在廊桥,用 $\times$ 表示该飞机停靠在远机位。
我们以表格中阴影部分的计算方式为例,说明该表的含义。在这一部分中,国际区有 $2$ 个廊桥,$4$ 架国际航班飞机依如下次序抵达:
1. 首先 $(2, 11)$ 在时刻 $2$ 抵达,停靠在廊桥。
2. 然后 $(4, 15)$ 在时刻 $4$ 抵达,停靠在另一个廊桥。
3. 接着 $(7, 17)$ 在时刻 $7$ 抵达,这时前 $2$ 架飞机都还没离开、都还占用着廊桥,而国际区只有 $2$ 个廊桥,所以只能停靠远机位。
4. 最后 $(12, 16)$ 在时刻 $12$ 抵达,这时 $(2, 11)$ 这架飞机已经离开,所以有 $1$ 个空闲的廊桥,该飞机可以停靠在廊桥。
根据表格中的计算结果,当国内区分配 $2$ 个廊桥、国际区分配 $1$ 个廊桥时,停靠廊桥的飞机数量最多,一共 $7$ 架。
**【样例解释 #2】**
当国内区分配 $2$ 个廊桥、国际区分配 $0$ 个廊桥时,停靠廊桥的飞机数量最多,一共 $4$ 架,即所有的国内航班飞机都能停靠在廊桥。
需要注意的是,本题中廊桥的使用遵循“先到先得”的原则,如果国际区只有 $1$ 个廊桥,那么将被飞机 $(1, 19)$ 占用,而不会被 $(3, 4)$、$(5, 6)$、$(7, 8)$、$(9, 10)$ 这 $4$ 架飞机先后使用。
**【数据范围】**
对于 $20 \%$ 的数据,$n \le 100$,$m_1 + m_2 \le 100$。
对于 $40 \%$ 的数据,$n \le 5000$,$m_1 + m_2 \le 5000$。
对于 $100 \%$ 的数据,$1 \le n \le {10}^5$,$m_1, m_2 \ge 1$,$m_1 + m_2 \le {10}^5$,所有 $a_{1, i}, b_{1, i}, a_{2, i}, b_{2, i}$ 为数值不超过 ${10}^8$ 的互不相同的正整数,且保证对于每个 $i \in [1, m_1]$,都有 $a_{1, i} < b_{1, i}$,以及对于每个 $i \in [1, m_2]$,都有 $a_{2, i} < b_{2, i}$。
解题思路
飞机到达时,有位置就停,没位置就不停。如果可以停,那么我们可以让他停在位置最小的,这样可以方便统计(统计到更多的飞机)。
(证明类似零件分组)
这样可以预处理出飞机分别停在哪个位置,并统计出每个位置的飞机数量,然后计算前缀和,枚举两国位置数量,即可打擂台求出最大值。
程序实现
逐个位置选择飞机,做法类似普及组T4!不断的寻找到达时间最接近上一架飞机离开时间的飞机,这些飞机用的是同一个位置。(感谢yangyang提供思路)
补充:虽然位置1的数量可能不是最多的,但如果可以更多,那么必然需要用到位置2,因为来得早却时间长的飞机有优先选择权,必会先使用廊桥。对于使用2个位置来说,飞机放到位置1或者位置2都是一样的。
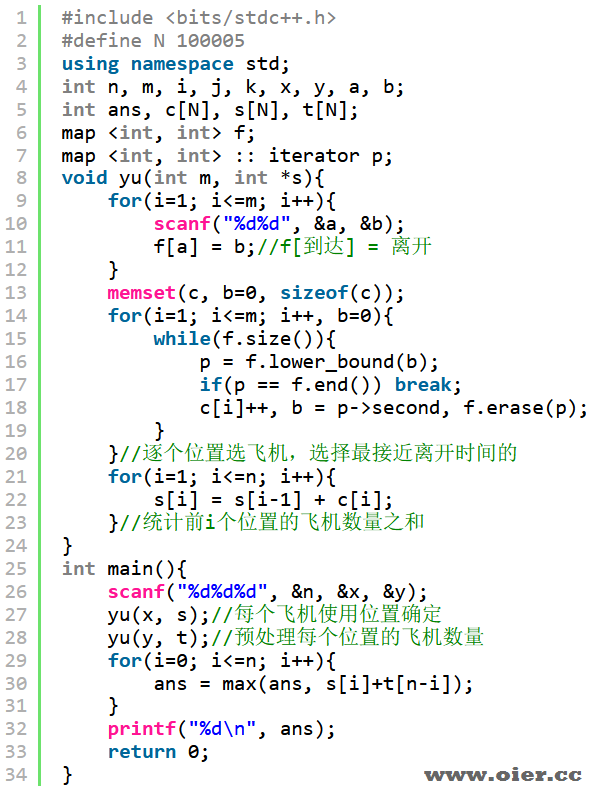
逐个飞机选择位置:将空闲位置放入堆中,即可log获取最小空闲位置;位置分配给飞机后,记录新的可用时间,只要可用时间小于下一架飞机到达时间,就可以用来停机,这里可以用map或者优先队列维护。(感谢huangjianheng提供思路)
