题目大意:n个柱子,每个柱子有m个球,共n种颜色,每种m个,有一个空的柱子n+1,怎么移动才能让颜色分好类?
题目描述
小 C 正在玩一个移球游戏,他面前有 根柱子,柱子从 编号,其中 号柱子、 号柱子、……、 号柱子上各有 个球,它们自底向上放置在柱子上, 号柱子上初始时没有球。这 个球共有 种颜色,每种颜色的球各 个。
初始时一根柱子上的球可能是五颜六色的,而小 C 的任务是将所有同种颜色的球移到同一根柱子上,这是唯一的目标,而每种颜色的球最后放置在哪根柱子则没有限制。
小 C 可以通过若干次操作完成这个目标,一次操作能将一个球从一根柱子移到另一根柱子上。更具体地,将 号柱子上的球移动到 号柱子上的要求为:
- 号柱子上至少有一个球;
- 号柱子上至多有 个球;
- 只能将 号柱子最上方的球移到 号柱子的最上方。
小 C 的目标并不难完成,因此他决定给自己加加难度:在完成目标的基础上,使用的操作次数不能超过 。换句话说,小 C 需要使用至多 次操作完成目标。
小 C 被难住了,但他相信难不倒你,请你给出一个操作方案完成小 C 的目标。合法的方案可能有多种,你只需要给出任意一种,题目保证一定存在一个合法方案。
输入格式
第一行两个用空格分隔的整数 。分别表示球的颜色数、每种颜色球的个数。
接下来 行每行 个用单个空格分隔的整数,第 行的整数按自底向上的顺序依次给出了 号柱子上的球的颜色。
输出格式
本题采用自定义校验器(special judge)评测。
你的输出的第一行应该仅包含单个整数 ,表示你的方案的操作次数。你应保证 。
接下来 行每行你应输出两个用单个空格分隔的正整数 ,表示这次操作将 号柱子最上方的球移动到 号柱子最上方。你应保证 且 。
输入输出样例
2 3 1 1 2 2 1 2
6 1 3 2 3 2 3 3 1 3 2 3 2
见附件中的 ball/ball2.in
见附件中的 ball/ball2.ans
见附件中的 ball/ball3.in
见附件中的 ball/ball3.ans
说明/提示
【样例 #1 解释】
柱子中的内容为:按自底向上的顺序依次给出柱子上每个球的颜色。
| 操作 | 号柱子 | 号柱子 | 号柱子 |
|---|---|---|---|
| 初始 | |||
【数据范围】
| 测试点编号 | ||
|---|---|---|
对于所有测试点,保证 ,。
【校验器】
为了方便选手测试,在附件中的 ball 目录下我们下发了 checker.cpp 文件,选手可以编译该程序,并使用它校验自己的输出文件。但请注意它与最终评测时所使用的校验器并不完全一致。你也不需要关心其代码的具体内容。
编译命令为:g++ checker.cpp −o checker -std=c++11。
checker 的使用方式为:checker <iuputfile> <outputfile>,参数依次表示输入文件与你的输出文件。
若你输出的数字大小范围不合法,则校验器会给出相应提示。若你的输出数字大小范围正确,但方案错误,则校验器会给出简要的错误信息:
A x,表示进行到第 个操作时不合法。B x,表示操作执行完毕后第 个柱子上的球不合法。
若你的方案正确,校验器会给出 OK。
解题思路
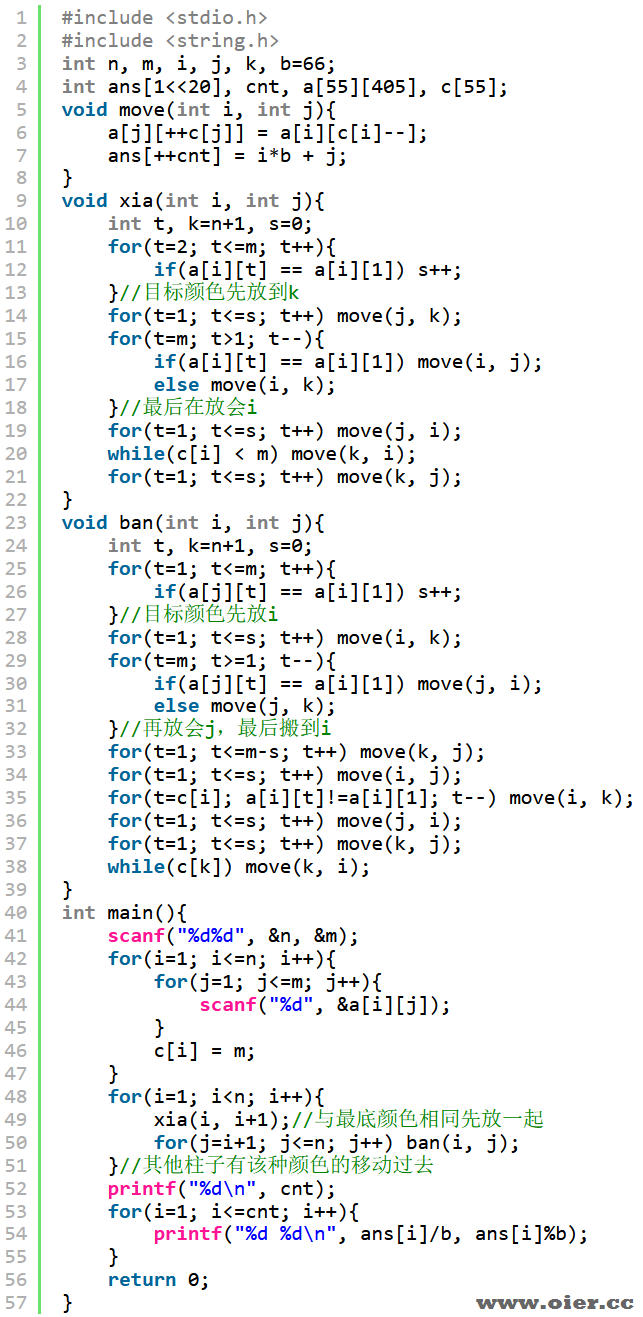
暴力思路:一种一种颜色去解决。第一根柱子,放跟最底球颜色相同的球,以此类推。有两个操作:一个是自己归类,将自己该放底层的球放在最底下;而是将其他柱子该颜色的球搬过来。
搬运特定颜色的球,操作很简单,只需要将目标颜色的球放在某根柱子顶端,最后清空该柱子,再放回去即可,如柱子i有s个目标球,我们可以借助j、k(空的)这样做:
1、j->k s个
2、i中目标球移到j,其他球移到k,此时j、k满
3、j->i s个
4、k原路搬回i、j,注意:需要保证i上面无目标球。
其他操作,总是很容易想到办法。
这样虽然是正确的,也不超时,但会超出限制次数,总的复杂度是O(n*n*m*常数),稳拿40分。
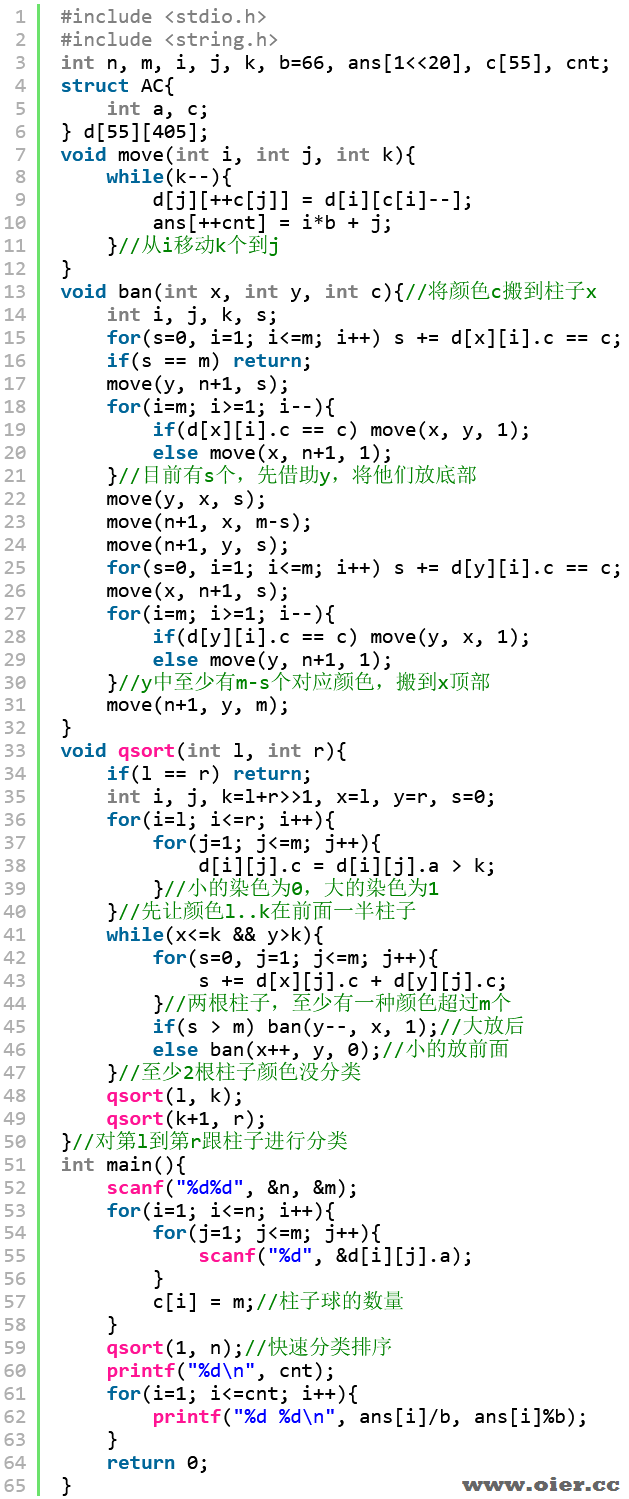
怎么样满分?分治!用快速排序的思想,由于数据均等,所以复杂度由n*n变nlog2n。
首先,我们可以将球分两类,颜色编号小的标为0,颜色标号大的标为1。归类的时候,0放在左边柱子,1放在右边柱子,这样不需要每种颜色都扫n个柱子。
最终排序的结果,就是颜色1在柱子1,颜色2在柱子2……
gsort(l, r)就是讲第l到第r根柱子进行归类,原来的颜色是a,重新编号为c,最终剩下1根柱子的时候,就排好序了!这时稳定的快速排序!
精华1:排序的时候,任选两根柱子,其中必有一种数字(0或1)达到m个,这时候,0放左边柱子,1放右边柱子;选柱子的时候,就选左右两半各一根。
精华2:移动次数绝不超过82万,首先是快速排序均分两份,共$log_250$层,约5~6趟;其次每次合并区间的两根柱子,第一层合并n-1次(剩下1根不需要合并);第二层合并n-2次;第三层合并n-4次……约节省n次合并。每次合并,常数是7m=2s+2m+3m,s<m,最极端也是$n*log_2n*m*7-m*n = 50*6*400*7-50*400 = 820000$,且不可能达到极端情况。
程序实现