题目大意:一个长度为n的数字序列,请问最长的满足条件的区间是多长?要求左端点唯一最小、右端点唯一最大!
题目描述
奶牛在熊大妈的带领下排成了一条直队。
显然,不同的奶牛身高不一定相同……
现在,奶牛们想知道,如果找出一些连续的奶牛,要求最左边的奶牛 $A$ 是最矮的,最右边的 $B$ 是最高的,且 $B$ 高于 $A$ 奶牛。中间如果存在奶牛,则身高不能和 $A,B$ 奶牛相同。问这样的奶牛最多会有多少头?
从左到右给出奶牛的身高,请告诉它们符合条件的最多的奶牛数(答案可能是 $0,2$,但不会是 $1$)。
输入输出格式
输入格式
第一行一个正整数 $N$,表示奶牛的头数。
接下来 $N$ 行,每行一个正整数,从上到下表示从左到右奶牛的身高 $h_i$。
输出格式
输入输出样例
输入样例 #1
5
1
2
3
4
1输出样例 #1
4说明
取第 $1$ 头到第 $4$ 头奶牛,满足条件且为最多。
对于全部的数据,$2 \le N \le 10^5$,$1 \le h_i <2^{31}$。
解题思路
此题可以用RMQ查询区间最大最小值,还可以用单调栈实现,时间复杂度分别是O(nlog2n)和O(n)。
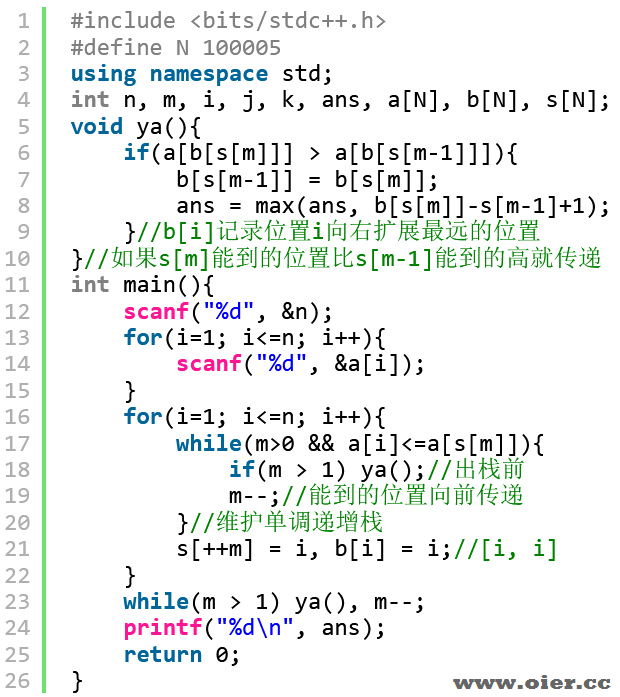
程序实现
RMQ方法容易理解、容易想到:解决这个问题,需要找区间[l, r]的最大值和最小值,我们不妨先找一个最大值作为区间的右端点R,显然相同大小去靠左边的,这样区间就分为[l, R]和[R+1, r]。接着我们在[l, R]找区间最小值作为区间的左端点L,显然相同大小找靠右边的。这样区间就分成3部分:
1、[l, L-1]:独立于右边的区间,因为L是最小值,所以其中每个元素都不能往右扩展。
2、[L, R]:最小值为L、最大值为R,且最值不重复,是满足要求的区间,记录最大长度即可。
3、[R+1, r]:独立于左边的区间,因为R是最大值,所以其中每个元素都不能向左扩展。
这个过程是O(1)的,区间长度至少减少1个,n次操作后即可找到答案。

单调栈是思考过程会比较痛苦,但效率却更高、代码更简洁明了。
首先,维护单独递增的栈,因为遇到递减,前面高的元素就不能往右扩展了。
接着,弹栈时需要维护信息。弹出的是m,那么m可以做完谁的左端点?逐个更新太慢,我们只更新新的栈顶,让他弹栈的时候,往回更新即可。
最后,细节问题。旧栈顶显然比新栈顶高,但更新是有前提条件的!
举个例子:1 3 8 15 11 10,单调栈得到1 3 8 11,10进栈时,11弹出来,却不能更新8!因为8被15更新过,且更大。因此,我们还需要开个数组,记录每个位置的元素,最远能扩展到哪里,更新时需要看是否是更高的,如果不是,说明中间有其他元素挡住他了。