题目大意:n米路,拆分成$a_1, a_2, a_3…$,要求序列a不递增,有多少种方案?
题目描述
小 H 是一个热爱运动的孩子,某天他想给自己制定一个跑步计划。小 H 计划跑 $n$ 米,其中第 $i(i \geq 1)$ 分钟要跑 $x_i$ 米($x_i$ 是正整数),但没有确定好总时长。
由于随着跑步时间增加,小 H 会越来越累,所以小 H 的计划必须满足对于任意 $i(i >1)$ 都满足 $x_i \leq x_{i-1}$。
现在小 H 想知道一共有多少个不同的满足条件的计划,请你帮助他。两个计划不同当且仅当跑步的总时长不同,或者存在一个 $i$,使得两个计划中 $x_i$ 不相同。
由于最后的答案可能很大,你只需要求出答案对 $p$ 取模的结果。
输入输出格式
输入格式
输出格式
输入输出样例
输入样例 #1
4 44
输出样例 #1
5输入样例 #2
66 666666
输出样例 #2
323522输入样例 #3
66666 66666666
输出样例 #3
45183149
说明
样例输入输出 1 解释
五个不同的计划分别是:$\{1,1,1,1\}$,$\{2,1,1\}$,$\{3,1\}$,$\{2,2\}$,$\{4\}$。
数据规模与约定
本题共 $10$ 个测试点,各测试点信息如下表。
| 测试点编号 | $n \leq$ | 测试点编号 | $n \leq$ |
| :———-: | :———: | :———-: | :———: |
| $1$ | $5$ | $6$ | $2\times 10^3$ |
| $2$ | $10$ | $7$ | $5\times 10^3$ |
| $3$ | $50$ | $8$ | $2\times 10^4$ |
| $4$ | $100$ | $9$ | $5\times 10^4$ |
| $5$ | $500$ | $10$ | $10^5$|
对于全部的测试点,保证 $1 \leq n \leq 10^5$,$1 \leq p < 2^{30}$。
解题思路
爆搜30,记忆化50,数学方法70,分块优化100。
程序实现
首先是暴力搜索,跟自然数拆分是同样的做法,不仅可以从大到小搜,还可以从小到大搜,方案数是一样的。
时间复杂度是组合数的复杂度,至少可得20分,实测30分。
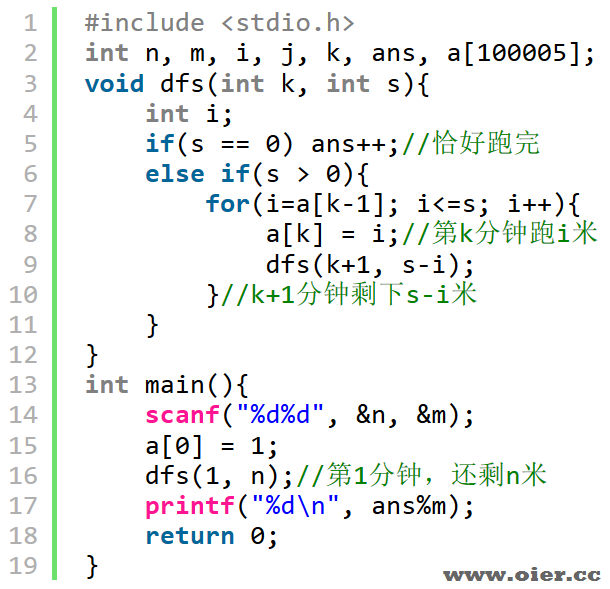
其次是加入记忆化,第k段路,前一段跑p米,还剩下s米,那么后面的情况(剩下s米,这次至少跑p米)是完全一样的,可以加入记忆化,避免重复调用自己。
时间复杂度:O(n*n*n),可得50分。
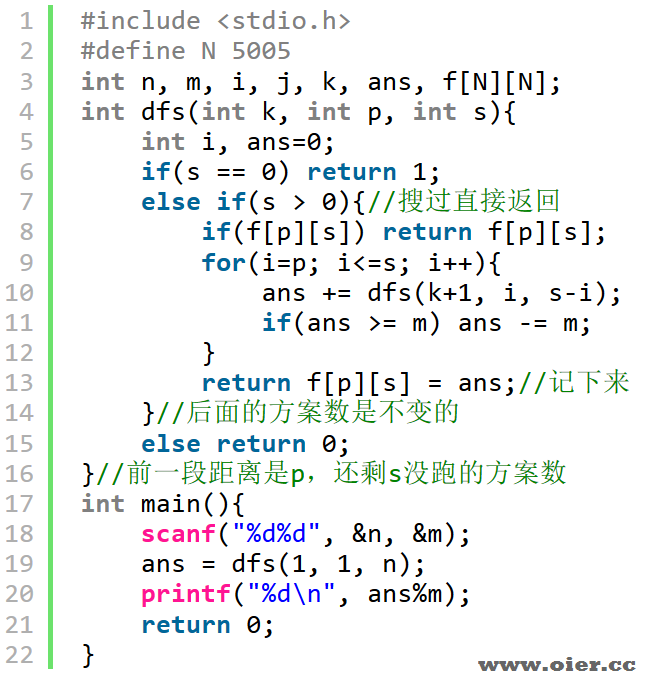
改变搜索对象,由搜索每一段路的距离,变成每一种长度的路有多少段!
因为代码第9行的循环,是每次加k的,所以时间复杂度跟筛法、调和级数有关:$O(n*n*log_2n)$,可得60分。
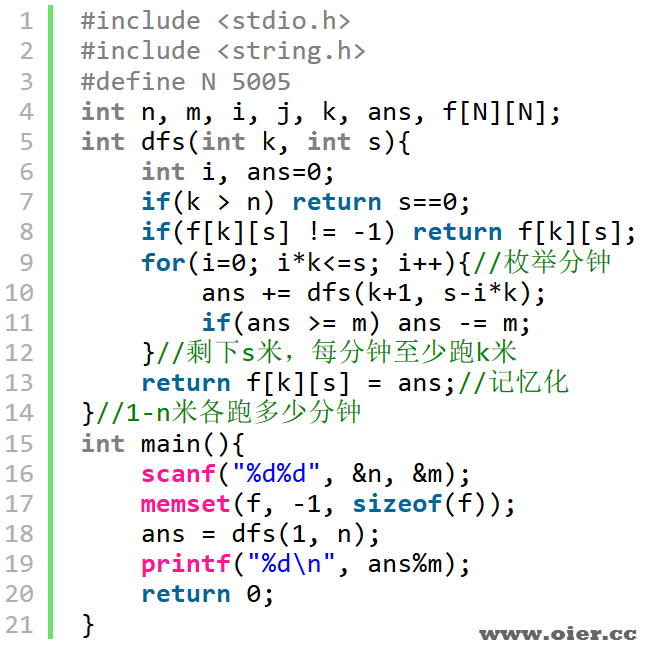
突然发现这是递推的模板?相当于n个相同的苹果,放入n个相同的盘子的方案数!n米路,每一米看成一个苹果;分到n段时间,每1分钟看成一个盘子!
递推:f[i][j]表示i个苹果放入j个盘子,要么全部盘子不空,由f[i-j][j]转移过来;要么至少一个盘子为空,由f[i][j-1]转移过来,所以f[i][j] = f[i-j][j] + f[i][j-1]。
时间复杂度:O(n*n),可得70分。

完全背包问题:每一种长度看成一个物品,可以选无限个,现在需要将n米装满!
时间复杂度:O(n*n),可得70分。

分块优化:因为n*n超时,所以需要优化。容量是很难变小的,但是物品则可以分类:小于$\sqrt{n}$和大于$\sqrt{n}$的。
对于小于的部分,我们可以跑完全背包。
对于大于的部分,我们可以再写个DP:g[i][j]表示长度为i,有j个大于等于m=$\sqrt{n}$的物品。转移也是分成两类:j个都是大于m和j个中至少1个不大于m。若j个都大于m,那么可以每一个减去1,还是有j个大于等于m(f[i-j][j]);若至少一个等于m,那么由j-1个新增1个m转移过来(f[i-m][j-1])。跟“放苹果”有点相似。
时间复杂度:$O(n\sqrt{n})$,可得满分。
