洛谷P5879放棋子[NOI导刊]
721+
题目大意：n行，第i行至多放i个棋子，且前一行的棋子不能比下一行的棋子多，至少放一个棋子，共有多少中放法？
题目描述
小虎刚刚上了幼儿园，老师让他做一个家庭作业：首先画 $3$ 行格子，第一行有三个格子，第二行有 $2$ 个格子，第三行有 $1$ 个格子。每行的格子从左到右可以放棋子，但要求除第一行外，每行放的棋子数不能超过上一行的棋子。第一行的棋子数不能为 $0$，但剩下行可以为空。玩了一会儿，小虎对哥哥大虎说：”这个作业有很多种摆放法，我想找到，但我不知道有多少种方案，你能帮助我吗？”
大虎是学校信息学集训队的，立刻想到用计算机来解决这个问题，并很快有了解答：$13$。
第二天他把问题拿到学校，并说如果第一行有 $N$ 个格子，第二行有 $N-1$ 个格子，……，第 $N$ 行有 $1$ 个格子，怎么办？现在请你一块来帮助他解决这个难题。
输入输出格式
输入格式
仅一行，一个正整数 $N$。
输出格式
一行，方案总数。
输入输出样例
输入样例 #1
2输出样例 #1
4输入样例 #2
3输出样例 #2
13说明
样例 1 说明：$N=2$ 时，有如下 $4$ 种摆放棋子法（ `*` 表示棋子，`_` 表示空格）：
| 方案数| 1 | 2 | 3 | 4 |
| :———– | :———– | :———– | :———– | :———– |
| **第一行** | `*_` | `**` | `*_` | `**` |
| **第二行** | `_` | `_` | `*` | `*` |对于 $30\%$ 数据：$1\le N\le 12$。
| 方案数| 1 | 2 | 3 | 4 |
| :———– | :———– | :———– | :———– | :———– |
| **第一行** | `*_` | `**` | `*_` | `**` |
| **第二行** | `_` | `_` | `*` | `*` |对于 $30\%$ 数据：$1\le N\le 12$。
对于 $50\%$ 数据：$1\le N\le 30$。
对于 $100\%$ 数据：$1\le N\le 100$。
解题思路
递推，f[i][j]表示第i行放j个棋子的方案数。首先赋初值，第一行可以放0个和1个；接下来，第i行至多放i个，放的棋子数j为1到i，上一行可以放k个，k的范围为0到j，用加法原理累加即可得50分。
程序实现
前缀和优化：f[i][j]表示第i行放棋子不超过j个的方案数，分两种情况，放不超过j-1个棋子，那么加上f[i][j-1]；放j个棋子，那么上一行不超过j个棋子，加上f[i-1][j]，然后判断j是否超过i-1。
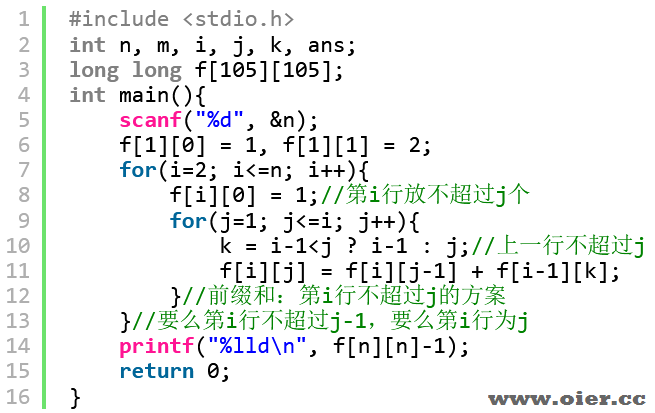
改成高精度即可满分。
