题目大意:求最小非负整数n,值得n%a[1]=b[1]、n%a[2]=b[2]、……、n%a[k]=b[k]。
题目描述
现有两组数字,每组k个,第一组中的数字分别为:a1,a2,…,ak表示,第二组中的数字分别用b1,b2,…,bk表示。其中第二组中的数字是两两互素的。求最小的非负整数n,满足对于任意的i,n – ai能被bi整除。
输入输出格式
输入格式:
输入数据的第一行是一个整数k,(1 ≤ k ≤ 10)。接下来有两行,第一行是:a1,a2,…,ak,第二行是b1,b2,…,bk
输出格式:
输出所求的整数n。
输入输出样例
3 1 2 3 2 3 5
23
说明
所有数据中,第一组数字的绝对值不超过109(可能为负数),第二组数字均为不超过6000的正整数,且第二组里所有数的乘积不超过1018
每个测试点时限1秒
注意:对于C/C++语言,对64位整型数应声明为long long,如使用scanf, printf函数(以及fscanf, fprintf等),应采用%lld标识符。
解题思路
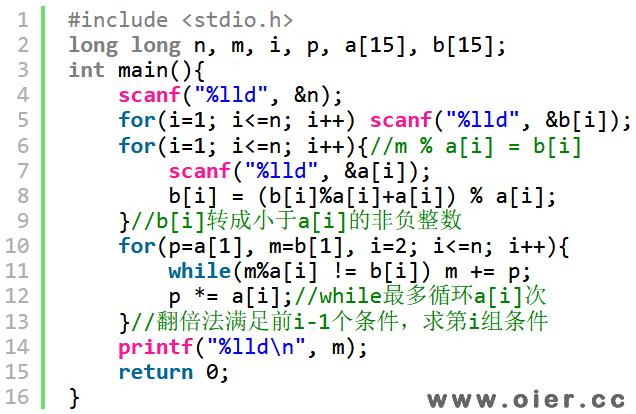
翻倍枚举,逐个条件解决。对于第一个条件,m取b[1]即可,因为b[1]%a[1] = b[1]。对于第二个条件,要满足m%a[2] = b[2],可以采用翻倍法逐个数字尝试,每次增加a[1],必能在a[2]次内找到一个数满足条件。因为每次增加a[1],m%a[1]还是等于b[1]。第三个条件,也可以这样出来,每次增加a[1]*a[2],在a[3]次内找到%a[3]=b[3]的数字,同时满足前两个条件……n次下来,n个条件都满足。时间复杂度是O(∑a[i])。
细节:a[i]范围比b[i]还大,读入b[i]后,可以先对a[i]取模,避免数字太大而出错;因为所有a[i]相乘不超过long long,所以必能在long long范围内找到一个符合要求的数字m。
程序实现
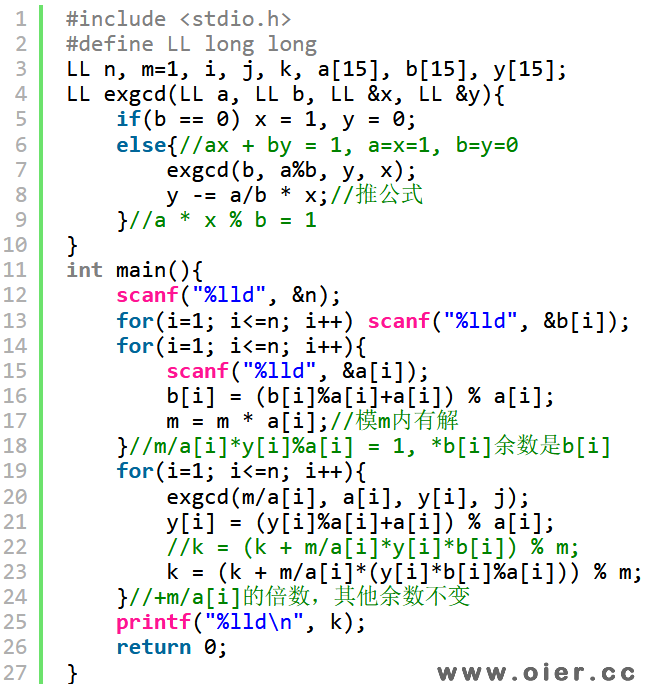
中国剩余定理:我们先考虑x%a[1]=b[1],且k是其他各个a[i]的倍数。为了方便,我们先求y%a[1]=1,再求x=y*b[1]即可。如何求y呢?y是a[2]*a[3]*…*a[n]的倍数,先让ji1=a[2]*a[3]*…*a[n],因为y%a[1]=1,只需要求出ji1模a[1]的逆元t1,那么y = ji1 * t1,x = ji1 * t1 * b[1]。安装这个方法,也可以求出x2、x3、x4、…、xn,这些x相加的和,就满足所有条件,因为x2到xn都是a[1]的倍数,%a[1]=0,加上x1后模a[1]余数就是b[1];x1、x3、x4…xn都是a[2]的倍数,加上x2后模a[2]余数就是b[2]……
注意,所有a[i]相乘在long long范围,代码22行,y[i]*b[i]可能超过a[i],也就是m/a[i]*y[i]*b[i]可能会超过long long,为避免丢分,最好还是将y[i]*b[i]模一下a[i]再相乘,以保证结果还是在long long范围内。时间复杂度O(nlog(ai))。