题目大意:给定正整数n和比n大的质数p,求1~n中所有整数在模p意义下的乘法逆元。
输入输出格式
输入格式:
一行n,p
输出格式:
n行,第i行表示i在模p意义下的逆元。
输入输出样例
输入样例#1:
10 13
输出样例#1:
1 7 9 10 8 11 2 5 3 4
说明
输入保证 为质数。
解题思路
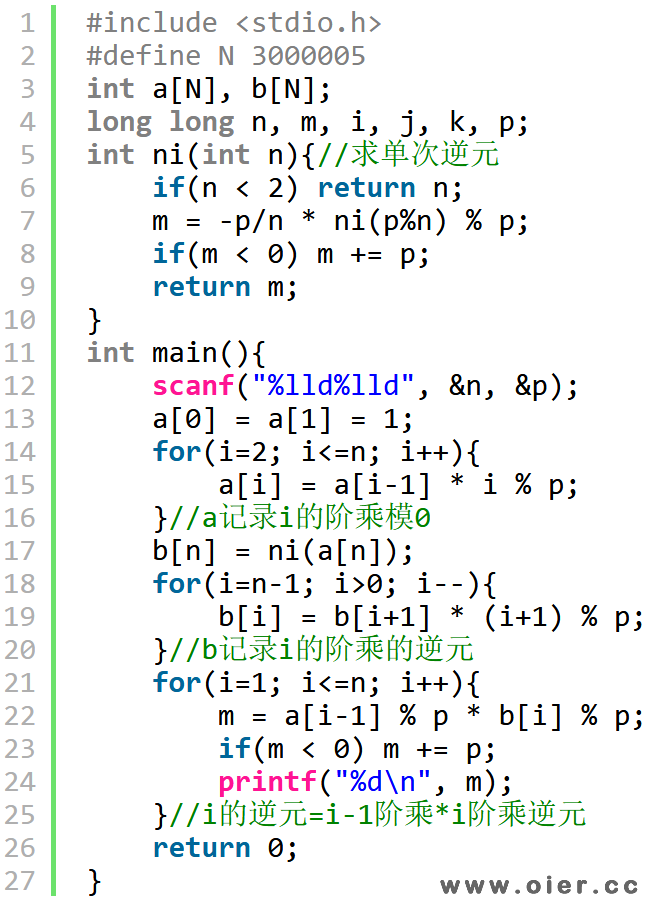
求逆元,可以用扩展欧几里得算法或者快速幂,由于需要求300万个数的逆元,每次求逆元的代价是log级别的话,可能会超时,因此我们只能采用线性的做法。
求i关于模p的逆元,i和p互质且i<p,另r = p % i,k = p / i,那么p = k*i + r,那么k*i + r = 0 (mod p)。
等式两边同时乘以和i-1r-1,可得到k*r-1 + i-1 = 0,i-1 = -k*r-1 = -p/i * r-1。
只要从小到大递推,即可用前面求出的逆元,求出后面的逆元。
程序实现
注意:p/i * a[p%i]可能会爆int,故p用了long long类型。
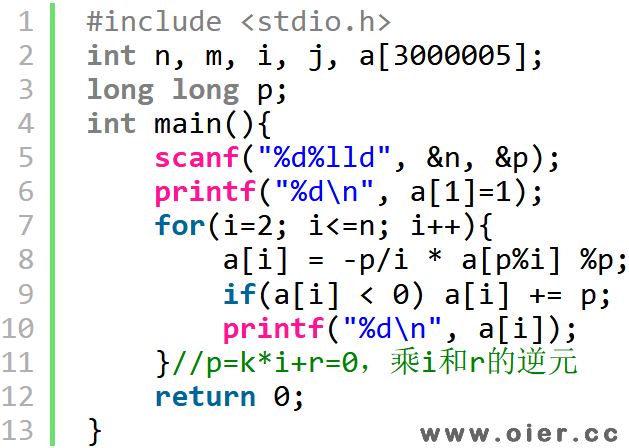
根据公式,可以转成递归的形式,用a数组记录逆元,计算过的直接范围,避免重复计算,时间复杂度也是线性的。
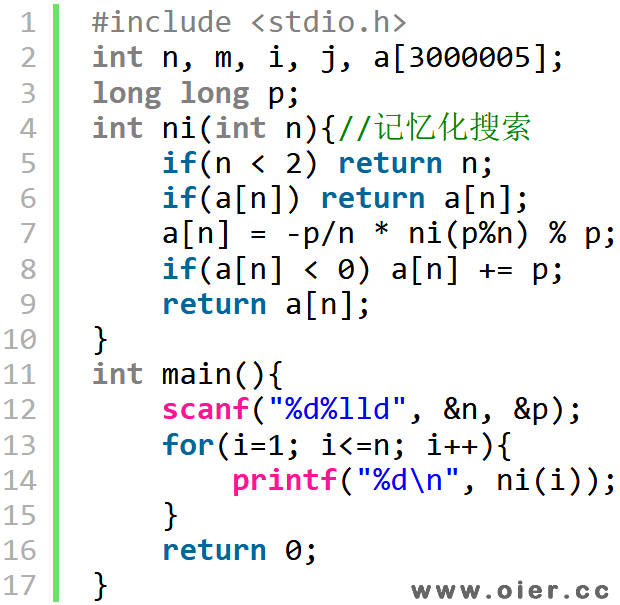
不用记忆化搜索,该公式也可以快速求出1个数的逆元。先计算n!的逆元,然后(n-1)!的逆元就等于n!的逆元*n,这样可以倒推出1到n每个数字的阶乘的逆元,从而计算n-1 = (n-1)! * n!-1。