题目大意:n个数的序列,不断对其某一段区间进行翻转,翻转m次后,这个序列变成什么样了?
题目背景
这是一道经典的Splay模板题——文艺平衡树。
题目描述
您需要写一种数据结构(可参考题目标题),来维护一个有序数列,其中需要提供以下操作:翻转一个区间,例如原有序序列是5 4 3 2 1,翻转区间是[2,4]的话,结果是5 2 3 4 1
输入输出格式
输入格式:
第一行为n,m n表示初始序列有n个数,这个序列依次是 m表示翻转操作次数
接下来m行每行两个数
输出格式:
输出一行n个数字,表示原始序列经过m次变换后的结果
输入输出样例
输入样例#1:
5 3 1 3 1 3 1 4
输出样例#1:
4 3 2 1 5
说明
解题思路
用一棵树的中序遍历表示一个序列,这个序列如果不是从小到大,那么他就不是一颗二叉排序树,用Treap就无法解决了,但Splay可以。Splay即伸展树,可以实现对一个序列进行区间翻转、赋值、加减等等操作,其每次操作的均摊复杂度是O(log2n)。
首先,如何对一个序列建立一棵Splay树呢?为了让一开始建立的Splay数比较平衡,可以选择中间的元素做根结点,左边区间放在左子树,右边区间放在右子树,递归建树即可。
其次,如何旋转才能保证序列不变且复杂度不退化?保证序列不变,结点一直旋转到根,旋转方法根Treap等是一样的:如左儿子旋转到父亲,那么左儿子的右儿子变为父亲,父亲的左儿子变为左儿子的原右儿子。那么,复杂度呢?每次访问一个结点,就把他旋转到根:如果还差一步就到根,就旋转一次;如果还差至少两步,那就两步两步旋转,之字形(非直线)的从下往上依次旋转(从上往下深度不变),直线形的先旋转父亲到祖父,再旋转儿子到父亲,避免退化。
思考:为什么复杂度均摊是log级别的?
具体证明有势能方法、会计方法等,比较难以理解。我们可以这样想,对于一颗平衡树,访问一个结点,深度是log级别的,往上旋转次数也是log级别的,旋转之后,且整棵树的高度不会增加,还是相对平衡的;在插入一个结点后,只要他旋转到根,就不会出现一条链(连续3个左/右子树为空)的情况。
接着是处理翻转操作。如果区间[x, y]需要翻转,那么我们可以把整棵树分成3不放,树a是区间[1, x-1],树b是区间[y+1, n],树R是区间[x, y],对其进行翻转,我们只需要打个翻转标记即可,输出时如果遇到翻转标记就下放,下放时还需要翻转一下左右子树。如何分离出a树和b树呢?将区间[1, n]第x个数旋转到根,其左子树就是a了,因为比根小的都在左边;同理,处理好个数等信息后,找原来的第y个数,旋转到根后,右子树就是树b了。
最后讲一下标记处理:在splay过程中,不需要管标记,因为每次都是先查找第k个再进行splay的。查找后,该结点及其祖先都没有翻转标记了,因为每次访问都会进行标记下放。
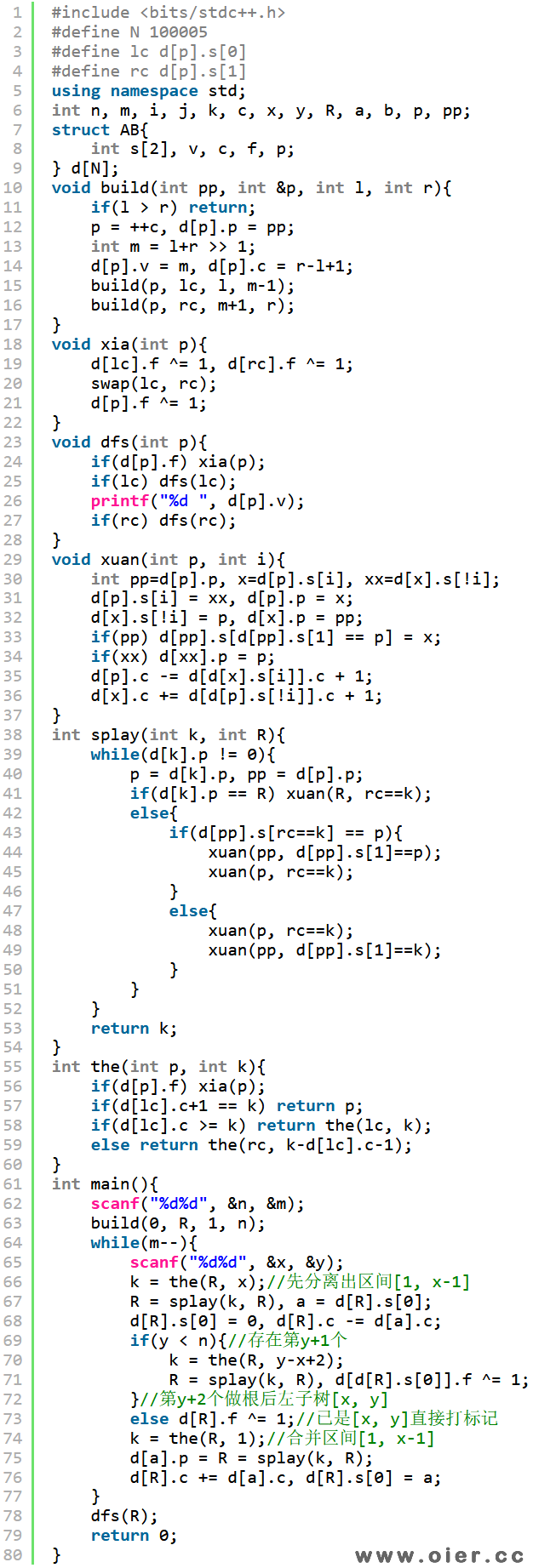
程序实现