题目大意:对于给出的m个在n范围的数,判断他们是不是素数;对于每个数,如果它是素数的话输出Yes,否则输出No。
题目描述
如题,给定一个范围N,你需要处理M个某数字是否为质数的询问(每个数字均在范围1-N内)
输入输出格式
输入格式:
第一行包含两个正整数N、M,分别表示查询的范围和查询的个数。
接下来M行每行包含一个不小于1且不大于N的整数,即询问概数是否为质数。
输出格式:
输出包含M行,每行为Yes或No,即依次为每一个询问的结果。
输入输出样例
输入样例#1:
100 5 2 3 4 91 97
输出样例#1:
Yes Yes No No Yes
说明
时空限制:500ms 128M
数据规模:
对于30%的数据:N<=10000,M<=10000
对于100%的数据:N<=10000000,M<=100000
样例说明:
N=100,说明接下来的询问数均不大于100且大于1。
所以2、3、97为质数,4、91非质数。
故依次输出Yes、Yes、No、No、Yes。
解题思路
大于1的数,不是素数就是合数。合数必有一个不大于他一半(或者说开平方)的质因子。因此,判断一个数是不是合数,只需要枚举一下,判断是否存在质因子(大于1的第一个因子必是质因子)。虽然时间复杂度不稳定,但偶数的判断只需要O(1)的复杂度,3的倍数的判断也比较快……
当然,也可以用筛选法求素数,预先处理好n以内的数,先假定他们都是素数,每遇到一个素数i,则将他的倍数j都筛掉(记为f[j]=0),如遇到2,筛掉“4 6 8 10 12 ……”,遇到3,筛掉“6 9 12 15 18……”等等,时间复杂度O(nlog2n+m),因为有m次询问,且2的倍数有n/2个,3的倍数有n/3个……即需要筛n/2 + n/3 + … + n/n= n * (1/2 + 1/3 + … + 1/n) = n*log2n次。
我们会发现,有些数被筛了多次,如6被2和3筛了,12被2、3、4、6筛了,这些重复是不必要的。如果每个数只被筛一次,这样复杂度就能降到O(n)了。因此,我们可以规定,每个数只能被他的最小质因子筛去,如6=2*3,被2筛;15=3*5,被3筛;36=2*2*3*3,被2筛,150=2*3*5*5,被2筛……如何做到呢?用s数组记录素数,x数组记录每个数的最小质因子。每进来一个素数,放入s数组中,该数的最小质因子就是自己;这样,每个素数的最小质因子都已知,合数的话在筛的时候记录;对于每个数i,枚举所有小于等于他的最小质因子的素数s[j],这样筛去的数i*s[j]必然只会被筛去一次,其最小质因子是s[j]。
程序实现
线性筛:
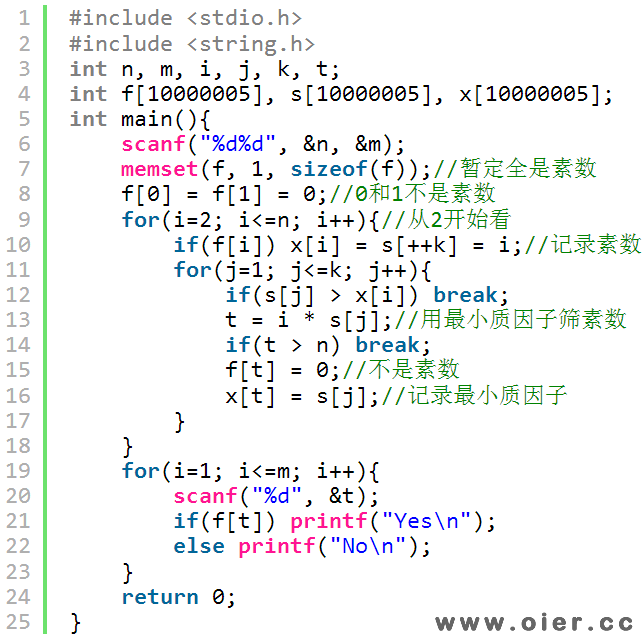
线性筛素数之所以有O(n)的时间复杂度,是因为每一个合数,分解成最小质因子和另外一个小于n的数,这个数t是唯一的!因此,在2到n枚举t,乘以不超过t最小质因子的质数,就可以得到其余合数。其实,记录最小质因子的x数组可以去掉,代码第10行,i%s[j]表示i中含有s[j]这个质因子,也就是说后面的质数都超过i的最小质因子了。

筛选法求素数:

逐个判断:
