题目大意:给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入输出格式
输入格式:
第一行包含三个正整数N、M、S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来N-1行每行包含两个正整数x、y,表示x结点和y结点之间有一条直接连接的边(数据保证可以构成树)。
接下来M行每行包含两个正整数a、b,表示询问a结点和b结点的最近公共祖先。
输出格式:
输出包含M行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例
输入样例#1:
5 5 4 3 1 2 4 5 1 1 4 2 4 3 2 3 5 1 2 4 5
输出样例#1:
4 4 1 4 4
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
解题思路
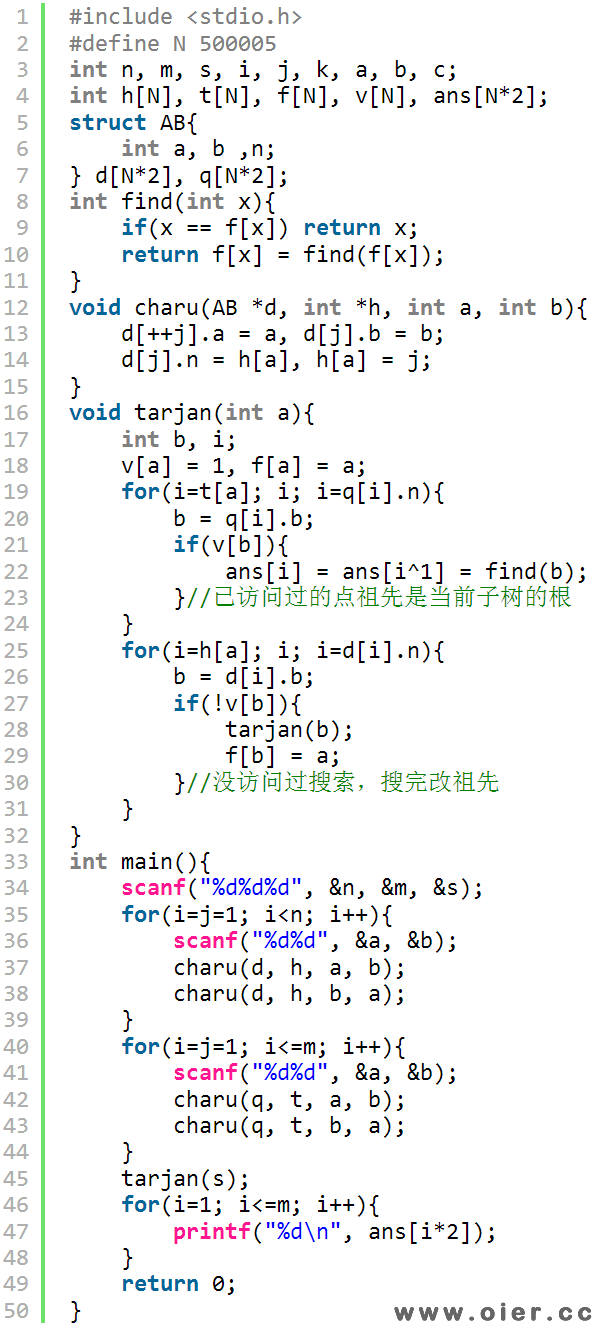
1、tarjan算法:这是一种离线算法,首先分别对边和询问建立邻接表,其原理是利用搜索的后续遍历,将搜索完的点的祖先修改成最小搜索子树的根,需要结合并查集。搜索过程中,先扫一遍与该点相关的询问,如果询问的另外一个点已经搜索过,那么该点的祖先就是当前最小搜索子树的根,也即最近公共祖先。接着再搜索该点的子树,搜索完的点更新自己的祖先为父亲结点。虽然自己的祖先总是自己或者父亲结点,但通过并查集可以快速压缩路径,找到最近公共祖先;虽然遍历某个点的询问时,有些点还没访问过,但是那些没访问过的点,总会被搜索到,这是这两个点的最近公共祖先也就能求出来。
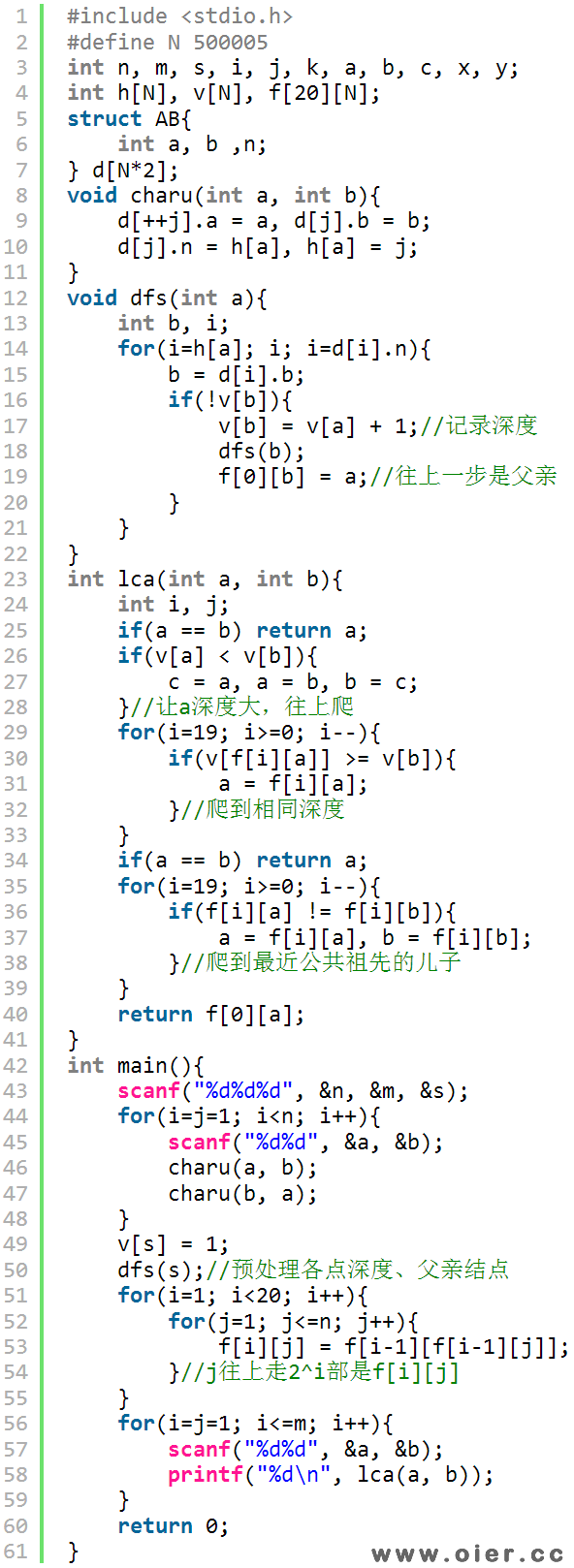
2、倍增算法:这是一种在线算法,首先建立边的邻接表,从跟开始搜索一步,预处理出各个点的深度和父亲结点;接着,预处理每个点往上走2步、4步、8步……分别到达那个结点,这样往上爬,速度比一步一步要快很多很多;最后就可以在线求两个点的最近公共祖先了,如果两个点深度不一样,让深度大的点先爬上去,使其深度一样,如果深度一样但不相同,那么公共祖先还在上面,就一起往上爬,直到爬到公共祖先的儿子,最后再爬一步就是公共祖先了。
问题1:为什么一直往上爬就能爬到深度相同?
不妨设深度差为x,那么x用二进制来表示,1的位置就怕对应2的多少次方不,必能爬到相同深度。
问题2:为什么最后只爬到最近公共祖先的儿子,不直接爬上去?
因为最近公共祖先上面的都是公共祖先,爬太高了,不能确定公共祖先是否是最近的。
问题3:为什么先爬2的19次方,再爬2的18次方……
因为先爬小的,不能确定是否是必须爬的。
程序实现