这是一道网络流模板题,文中提供了深度搜索和广度搜索的代码,其中广度搜索会快很多。
题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入样例#1:
4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40
输出样例#1:
50
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明
题目中存在3条路径:
4–>2–>3,该路线可通过20的流量
4–>3,可通过20的流量
4–>2–>1–>3,可通过10的流量(边4–>2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
简单分析
网络流,好比是一个城市道路,每条路限制了日运输量,求从城市s到城市t,每天最多运多少货物过去。
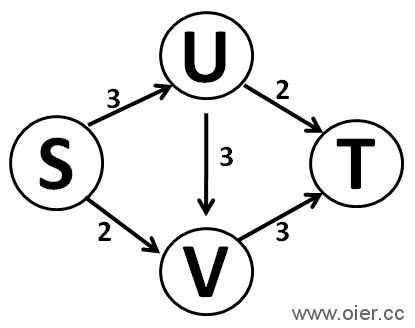
如果能运一次,答案是3,S→U→V→T这条路一次性运3
如果能运两次:答案是4,S→U→T和S→V→T这两条路各运一次,分别运2。
现在是不限运输次数,每次只需要找一下有没有路可以从S到达T就行了。因此,每次找到一条路,在记录运输量的同时,要把这条路径上的运输量减小。如上述例子,每次选择的路径是随机的,并不能保证选了之后会出现最优解,如选了S→U→V→T这条路一次性运3后,就不能再运输了。为了纠正这种错误,我们为图增加后向弧:原来U→V可以运输3,就增加一条V→U可以运输0的边,这对原来不会有影响;U→V运输了3以后,运输量变为0,而V→U变为3,即下次你后悔从U→V运输了的话,可以走V→U反悔。
这样,问题就可以转化为不断找S到T的路径的问题了。每次从S出发,找到达T的路径,如果能到达,则更新运输量,同时,S的出边运输量降低;直到不可到达时,就不可能再找到路径了。
注意赋初值:S点原来货物很多很多,接近无穷大;每次搜索找路径,走过的都不要再走,搜索前标记没走过;巧妙记录正向边反向边,方便更新他们的运输量……
程序实现
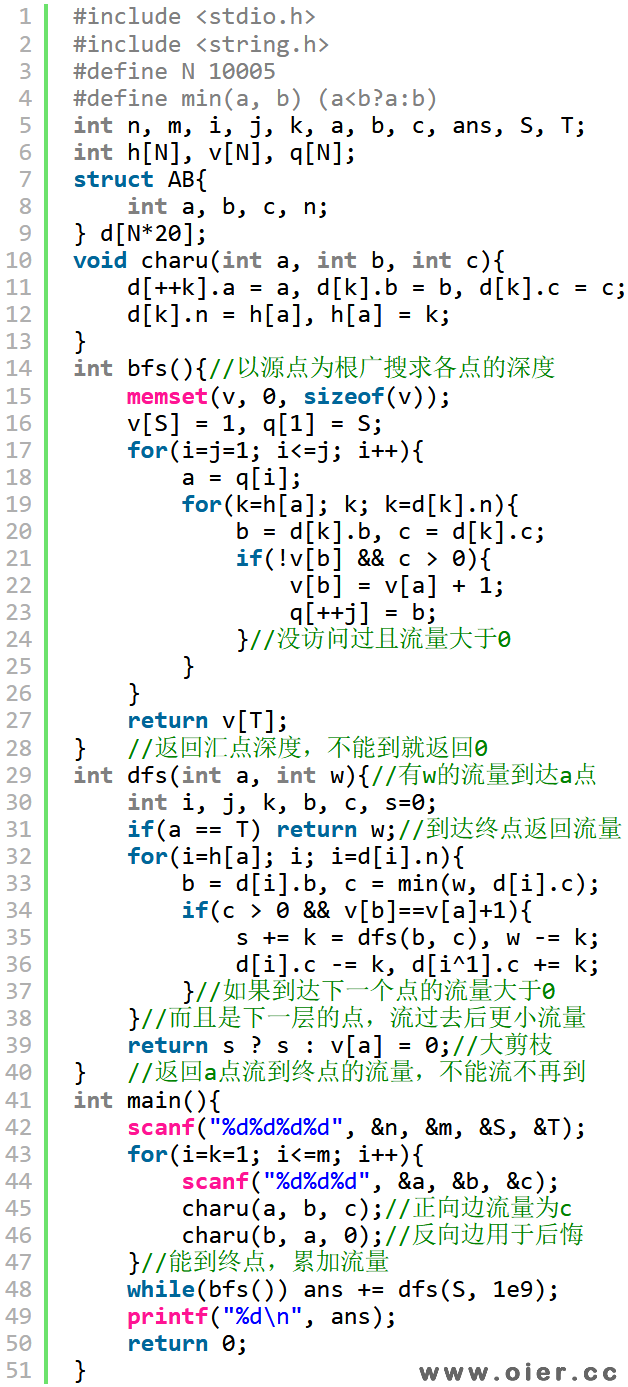
1、深度搜索,90分
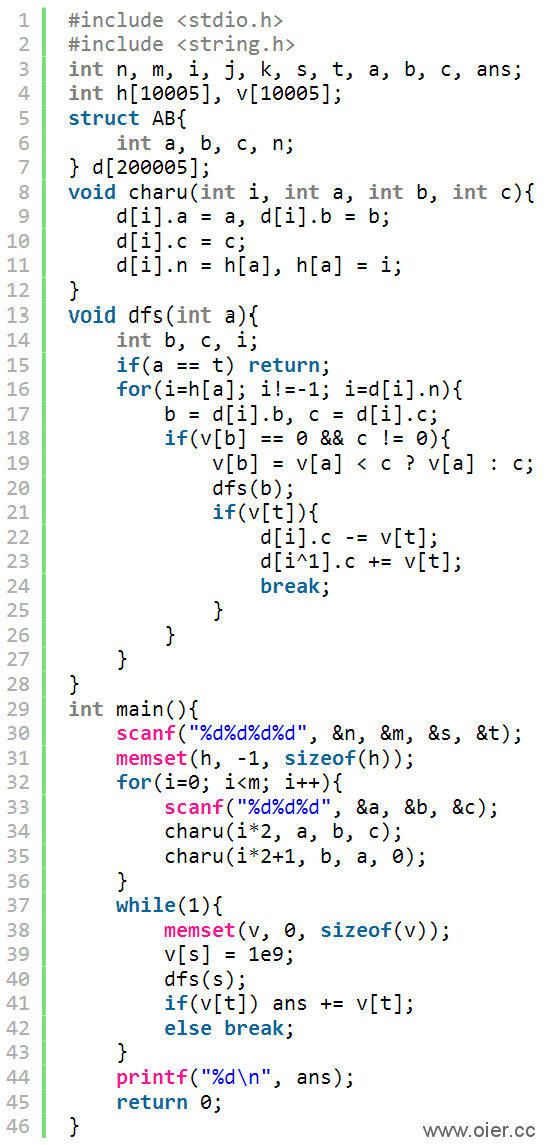
2、广度搜索,每个点都访问一下,1500ms
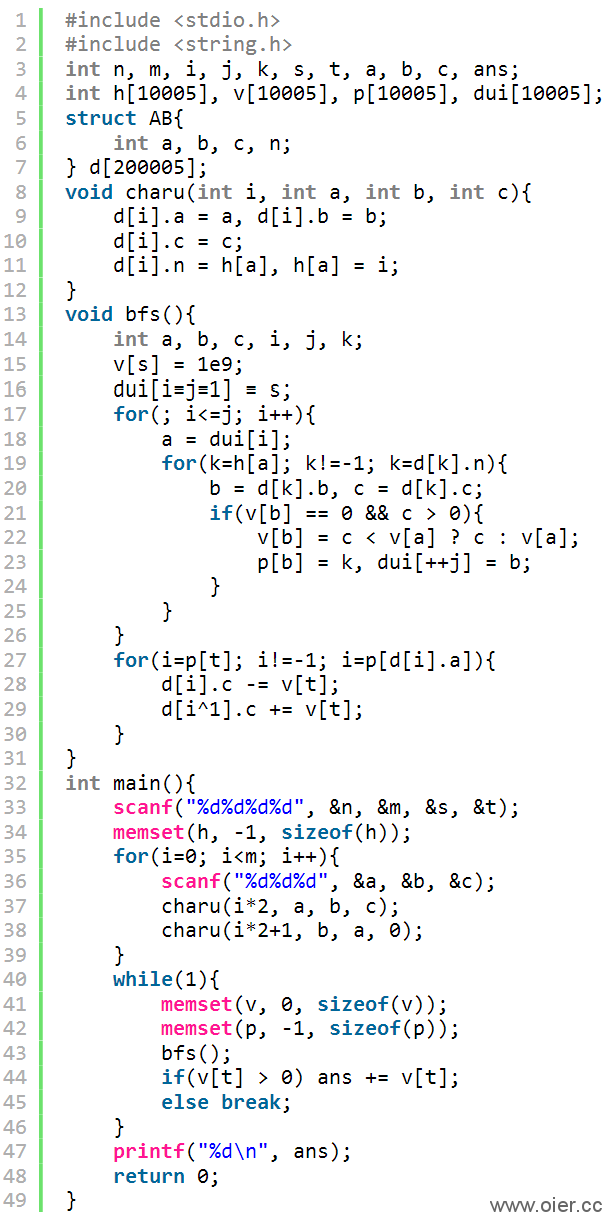
3、广度搜索,走到终点就停下来,800ms
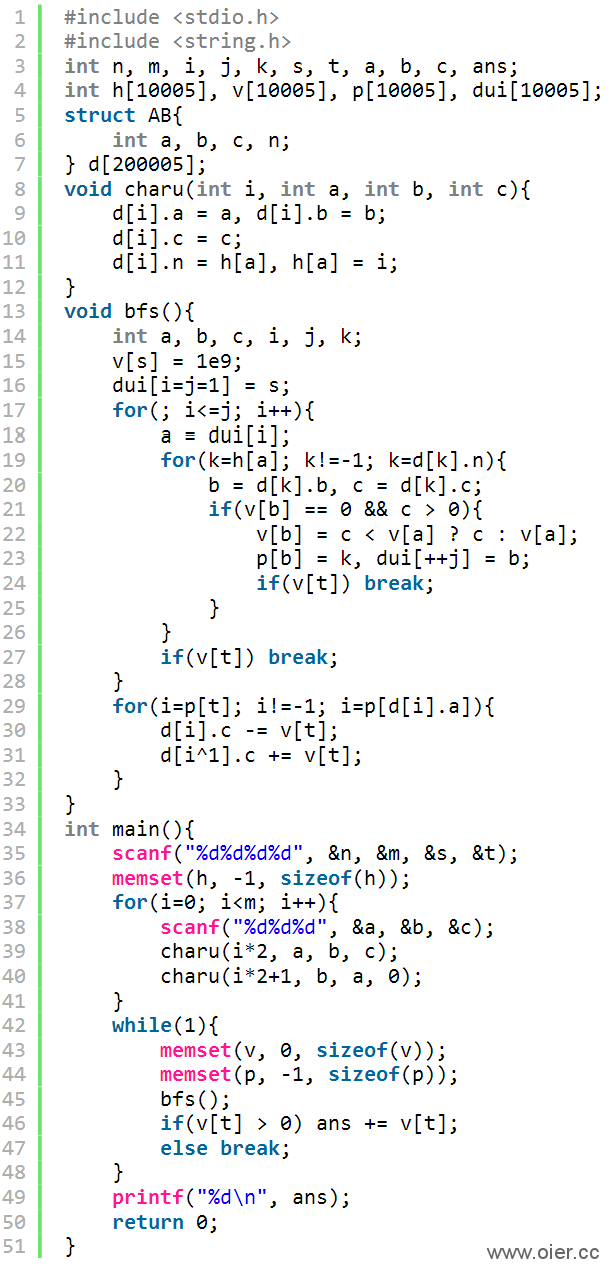
4、Dinic算法求最大流:以上算法,深搜一次或者广搜一次,只能增广一次,其复杂度与增广次数有关。Dinic算法,结合bfs和dfs的优势,通过一次搜索,多次增广,提高效率。
首先,以源点为根,bfs预处理其他各个点的深度,dfs的时候,到的下一个点必定是下一层的(下一个点的深度=前一个点深度+1),这样就避免了一个点重复到另外一个点的情况,而且搜索深度也会减小。当然,这样并不能提高速度,因为增广一次复杂度同样是O(m+n)。要真的提高效率,就要增广多次:dfs(a, w)表示有w的流量到达a点,返回的是从a点运输了多少流量到终点。由于只往深度大的点走,就不会走回头,a点通过一条路径运输完流量到终点后,可以继续找下一条路径继续运输流量,需要注意的是,回溯的时候,要更新正向边和反向边以及w的流量。
dfs代码中,a是起点,b是下一个点,c的能到b的流量,其大小取决于w和边的容量,取两者中小的一个。如果有流量到b且b是下一层,才尝试通过b运输流量到汇点,如果能运输到汇点,那么k就是运输的流量大小,那么从a到会得到流量s要增加a,停留在a的流量w要减少k,同时正向边减少k,反向边增加k。每条边都试过以后,返回从a点到达汇点的流量s。
当然,代码39行有个剪枝,如果s为0,说明有流量到了a点,但从a点出发,已经不能运输流量到汇点了,下次就不需要再到a了,将其深度标记为0就不会等于前一个点深度+1,就不会再走这个点了。这样速度至少快一倍,对于一下特殊的图甚至快好几十倍,可以避免超时。
5、Dinic稳定DFS:上面的Dinic代码,dfs的时候时间并不稳定,因为可能出现在路径后面出现不能到的情况,但前面的点还一直往这条路走。如果让dfs复杂度稳定呢?每条边只走一次!当然,这也要保证一次bfs后可以多次增广,不然预处理就没意义了。如果实现每条边只走一次呢?而且不要重复判断一条边有没有走过,因为一个点可以访问多次。可以这样做:用完点a一条边后,h[a]就跳到下一条边,即使下次再到达a点,访问过的边也不会再访问了。实现方法:int &i=h[a],这样i修改的时候,h[a]就会跟着修改,需要注意的是,修改h[a]后,下次要用的话需要恢复一下h的数据。
代码中为什么dfs一次只找一条路?首先,多次dfs的时间复杂度还是O(m+n),一次bfs后可以增广多次,增广多次的复杂度也是O(m+n)。为什么不像上面代码那样,一次dfs增广多次呢?因为一次dfs增广多次,留在每个点的流量会越来越小,可能有些边本来可以增广更大流量的,结果却增广了小流量,会间接地增加bfs的次数,降低速度。
