题目大意:n个点m条边,请问第x点到其他各个点的最短路径分别是多少?
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入输出格式
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
输入输出样例
输入样例#1:
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
输出样例#1:
0 2 4 3
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15
对于40%的数据:N<=100,M<=10000
对于70%的数据:N<=1000,M<=100000
对于100%的数据:N<=10000,M<=500000
解题思路
求单源最短路径,由于点个数很多,边相对少,是稀疏图,直接用迪杰斯特拉算法,n方复杂度会超时,故使用SPFA或者堆优化的迪杰斯特拉更为妥当。
程序实现
1、SPFA算法:起始点入队后,出队不断更新到其他点的距离,有更近的,则需要重新入队出队再次更新到其他点的距离,直到各个点的距离都不能再近为止。跟bfs很相似,注意是多了一个u数组,记录当前点是否在队列中,如果在的话,就只更新距离,不重复入队了。

2、SLF优化:在SPFA的基础上,各个点有更近距离时,入队可以选择队头,也可以选择队尾,尽量把距离小的点放在队头,这样近的点先更新,能一定程度上减少重复入队的次数。

3、堆优化:以下程序,你可以看成是SPAF的堆优化,但这里不再使用u数组了(你硬要用u数组也行),而是更近就入队,根据最近点的距离判断是否需要继续更新距离,保证每条边只处理一次;你也可以看成是迪杰斯特拉的堆优化程序,每次选一个离起始点最近的点(这个点不会被其他点更新了),去更新起始点到其他点的距离。程序之所以要重复入队,是因为更新堆(优先队列)里面的结点的值比较困难。时间复杂度:O(mlog2(m)),因为每条边最多访问一次,最多入队m次、出队m次。
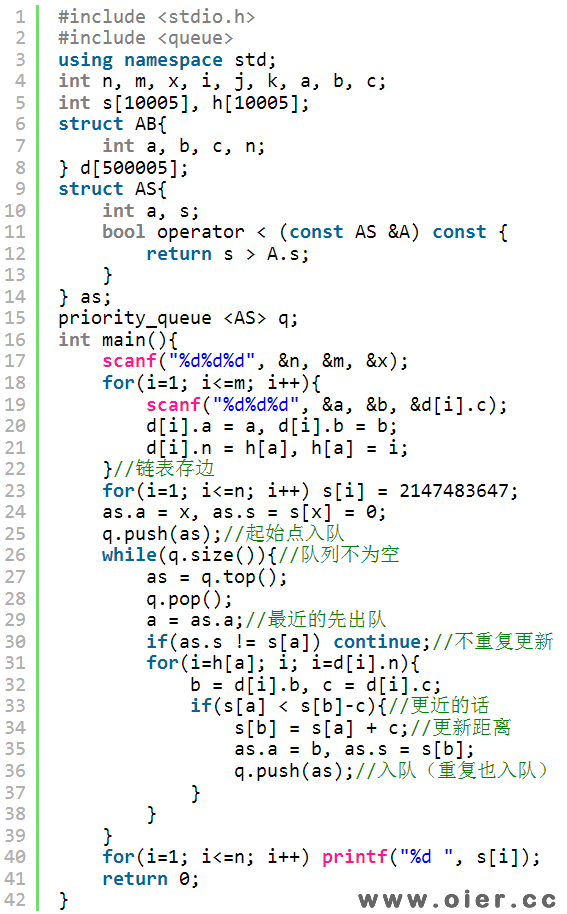
4、其他:你也可以考虑对链表中的边进行排序,让队列中更多的点是从近到远的……