题目大意:若干个数依次添加/删除,随时回答排名为x的数是多少,或者数x的排名、数x的前驱后继等问题。
题目描述
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入x数
- 删除x数(若有多个相同的数,因只删除一个)
- 查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数,因输出最小的排名)
- 查询排名为x的数
- 求x的前驱(前驱定义为小于x,且最大的数)
- 求x的后继(后继定义为大于x,且最小的数)
输入输出格式
输入格式:
第一行为n,表示操作的个数,下面n行每行有两个数opt和x,opt表示操作的序号( )
输出格式:
对于操作3,4,5,6每行输出一个数,表示对应答案
输入输出样例
输入样例#1:
10 1 106465 4 1 1 317721 1 460929 1 644985 1 84185 1 89851 6 81968 1 492737 5 493598
输出样例#1:
106465 84185 492737
说明
时空限制:1000ms,128M
1.n的数据范围:
2.每个数的数据范围:
解题思路
用树状数组统计每个数出现的次数,求数x的排名,也就是求比x小的数有多少个,he(x-1) + 1即排名;寻找排名为x的数n,那么前n个数字出现总次数最先大于等于x,通过二分树状数组可以得到;寻找x的前驱,也就是排名比x少1的那个数,排名为he(x-1);x的后继,就是比x大一点点的那个数,排名为he(x)+1。为了避免出现负数,我们可以让所有数字加上1千万!
程序实现
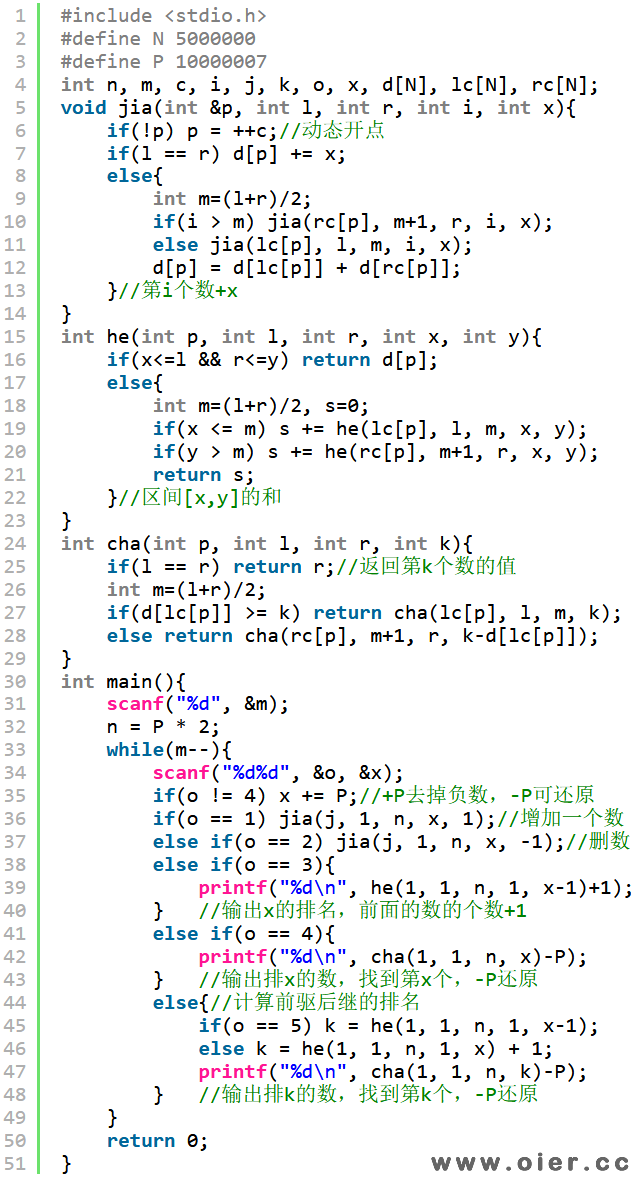
树状数组

线段树
离散化+树状数组

Treap:Tree+Heap,首先是一棵排序二叉树,中序遍历是有序的,其次是个堆,根结点的优先级不大于儿子结点的优先级。结点数据:值key、优先级pri、子树个数size、左右儿子son[0]和son[1]。排序二叉树有可能退化成一条链的情况,但是随机生成的数据几乎不会有退化,我们可以给每个结点随机一个优先级,让这个二叉排序树的优先级满足堆的性质,这样就相当于随机数据下建立的排序二叉树了,要保持排序二叉树和堆的性质,可以通过旋转来实现。
插入节点:代码15行,按照二叉排序树,找到结点插入的位置;代码23行,如果发现插入的结点,会导致不满足堆的性质,通过旋转维护,把优先级小的旋转到根。
删除结点:代码27行,如果找到对应的结点,如果要删除的结点没有空结点,那么把优先级小的旋转上去,自己旋转下去后继续删除;如果有空结点,把非空结点优先级小的点直接接上去就行。代码37-39行,查找待删除结点的位置,判断在左边还是右边,然后进去子树删除。
小于k的结点个数:如果根结点小于k,那么左子树以及根都小于k,累加个数,然后再看看右边有多少个小于k的;如果根结点不小于k,那么小于k的结点个数都在左子树,直接在左子树统计就行;边界条件,空结点个数为0。k的排名,就是小于k的结点数加1。(求小于等于k的结点个数同理)
第k个:在子树中找第k个,如果左子树有x个,那么根结点是第x+1个,如x+1==k,返回根结点;如果x>=k,那么在左子树找;如果x<k,那么以及找到x+1个比k小的,在右子树继续找第k-x-1个。
前驱后继:小于k的个数是x,小于等于k的个数是y,那么前驱就是第x个,后继就是第y+1个。
旋转技巧:如果左儿子s旋转到父亲结点p,那么p的lc该改成s的rc,s的rc要改成p;如果右儿子s旋转到父亲结点p,那么p的rc该改成s的lc,s的lc要改成p。lc和rc切换,可以转换成0和1的切换。p的儿子0要旋转上来,那么p的儿子0要改成儿子0的儿子1,儿子0的儿子1要改成p,中间多次用到儿子0,需要注意顺序,可以用top记录原来的儿子0,也即新的根。如果是右儿子旋转,只需要把0改成1,1改成0,如果c是记录儿子编号,直接用c和!c就可以完美解决。
子树大小:每增加一个结点,所有祖先结点个数要加1(代码21行);每删除一个结点,所有祖先结点个数要减1(代码31和38行);旋转过程中,完美只需要修改新旧根结点的个数即可,旧的根结点,结点个数少了同方向上孙子树的结点个数+1个;新的根结点结点个数多了兄弟结点个数+1个。(相同方向,c还是c;相反方向,c改成!c;兄弟结点,即另外一个儿子,即!c)
引用真奇妙:修改和删除都用引用&p记录子树根结点,每次旋转或者删除完毕后,修改p的值,也就是修改了p的父亲对应的儿子的编号,因为p都是通过儿子编号传过来的。
