题目大意:n名飞行员,A国籍有a人,B国籍有b人,已知A中哪些人可以跟B中哪些人合作,现在需要不同国籍的飞行员搭配,最多有多少个配对?
题目背景
第二次世界大战时期..
题目描述
英国皇家空军从沦陷国征募了大量外籍飞行员。由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的2 名飞行员,其中1 名是英国飞行员,另1名是外籍飞行员。在众多的飞行员中,每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。如何选择配对飞行的飞行员才能使一次派出最多的飞机。对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
对于给定的外籍飞行员与英国飞行员的配合情况,编程找出一个最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
输入输出格式
输入格式:
第 1 行有 2 个正整数 m 和 n。n 是皇家空军的飞行员总数(n<100);m 是外籍飞行员数(m<=n)。外籍飞行员编号为 1~m;英国飞行员编号为 m+1~n。
接下来每行有 2 个正整数 i 和 j,表示外籍飞行员 i 可以和英国飞行员 j 配合。最后以 2个-1 结束。
输出格式:
第 1 行是最佳飞行员配对方案一次能派出的最多的飞机数 M。接下来 M 行是最佳飞行员配对方案。每行有 2个正整数 i 和 j,表示在最佳飞行员配对方案中,飞行员 i 和飞行员 j 配对。如果所求的最佳飞行员配对方案不存在,则输出‘No Solution!’。
输入输出样例
解题思路
二分图最大匹配,可以用匈牙利算法:将飞行员划分成2大集合,外籍是A集合,英国籍是B集合,如果两人可以合作,那么A集合对应的飞行员向B集合对应的飞行员连一条有向边,因为我们只需要为A集合找合作伙伴就行,A集合找完后,B集合就自动找完了;建边后,对外籍每一个飞行员a进行搜索查找合作伙伴——与他有边的英国飞行员b,如果还没有跟其他飞行员配对,那么他们就可以直接配对,如果已经跟另外一个外籍飞行员pb配对,那么看一下另外那个外籍飞行员pb是否可以和另外一个英国飞行员配对,如果可以那就让他们配对,之后a就能够和b配对了。
dfs函数是判断外籍飞行员a是否可以跟英国飞行员配对,可以返回非0值,不可以返回0。配对过程中,如果发现pb不可以换人(如果可以换人,后面也会找到解决方案),那么b就注定要跟pb配对了,因为如果b跟其他人配对,pb就无法配对,即使a和b配对成功,匹配数量还是没有变大。17行v[b]=1是记录已经尝试过让pb换人了,下次就不需要再试了,因为从pb出发也找不到没配对过的B集合的点了,保证了每次搜索的时间复杂度是O(m+n),同时也避免了重复换人死循环。
32行代码每次给A集合的点匹配的时候都执行,是因为v记录的是前1个点不能换人的情况,但多了一个点后,可能能走更远:如1→1、1→3、2→1、2→2、2→3、3→3、3→4、4→1,先找到1→1和2→3两个匹配,如果从3出发先找3,然后2再找1,发现1找不到其他点与他匹配(因为3访问过了,再访问不就有可能死循环?虽然2可以换其他点,但后面2会继续找),但此时并不能断定1再也找不到匹配了,接着2找到2,得到3个匹配1→1、2→2、3→3。后来4找1进行匹配,因为通过3可以到达其他未匹配的点。因此,v记录的是在某个点找匹配的时候,哪些点已经访问过了。我们可以让v不只是等于1,让他等于寻找匹配的那个点,搜索过程中,如果v的值等于正在寻找匹配的点,那么就不用找了,因为之前已经为这个点找过了,否则才找,这样就不需要每次memset了。
程序实现
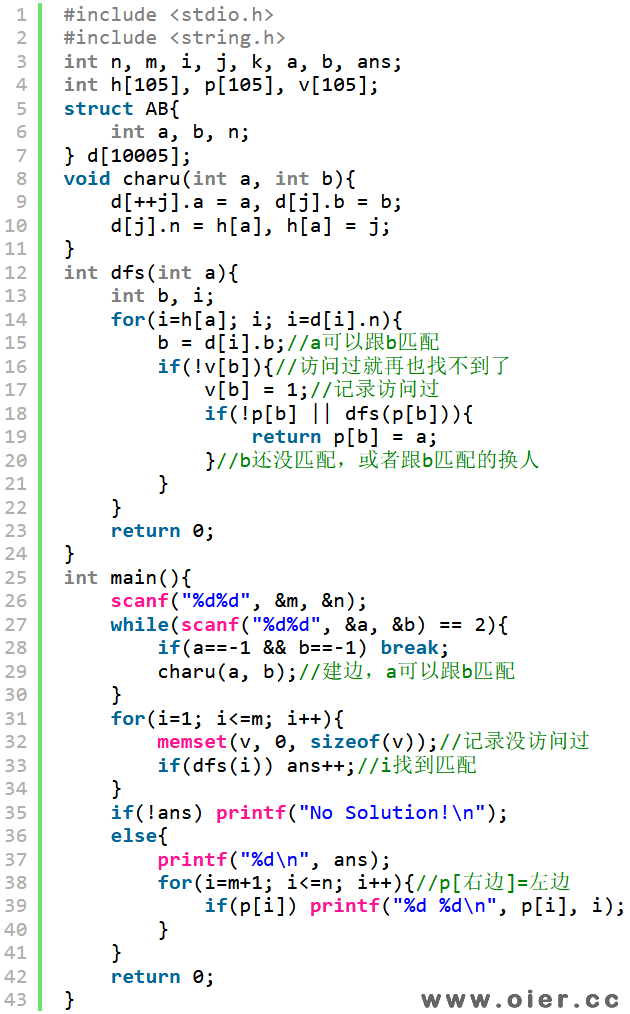
时间戳
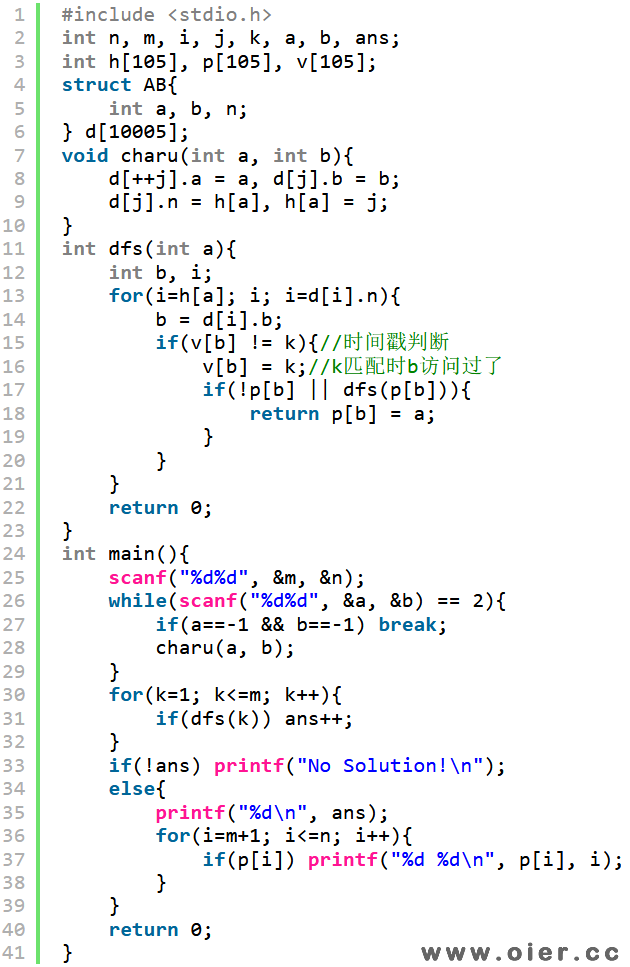
网络流:S向外籍连边,英国籍向T连边,外籍向英国籍连边,所有边权为1,反向边权值为0,从S到T必须经过国籍有向边,这样流量即是边数、匹配数,因为他保证了每条国籍边只用1次,而且每个飞行员也只用1次。。
