题目大意:一棵树上,每条边都有一个权值,连接两个结点之间的所有边的权值异或之后是多少?
题目描述
异或是一种神奇的运算,大部分人把它总结成不进位加法.
在生活中…xor运算也很常见。比如,对于一个问题的回答,是为1,否为0.那么:
(A是否是男生 )xor( B是否是男生)=A和B是否能够成为情侣
好了,现在我们来制造和处理一些复杂的情况。比如我们将给出一颗树,它很高兴自己有N个结点。树的每条边上有一个权值。我们要进行M次询问,对于每次询问,我们想知道某两点之间的路径上所有边权的异或值。
输入输出格式
输入格式:
输入文件第一行包含一个整数N,表示这颗开心的树拥有的结点数,以下有N-1行,描述这些边,每行有3个数,u,v,w,表示u和v之间有一条权值为w的边。接下来一行有一个整数M,表示询问数。之后的M行,每行两个数u,v,表示询问这两个点之间的路径上的权值异或值。
输出格式:
输出M行,每行一个整数,表示异或值
输入输出样例
输入样例#1:
5 1 4 9644 2 5 15004 3 1 14635 5 3 9684 3 2 4 5 4 1 1
输出样例#1:
975 14675 0
说明
对于40%的数据,有1 ≤ N,M ≤ 3000;
对于100%的数据,有1 ≤ N ,M≤ 100000。
解题思路
看到这道题,很容易想到求最近公共祖先。
不妨设根结点是g,要查询的两个结点分别是a和b,a和b的最近公共祖先是c。我们可以先预处理所有节点到根结点的异或指,这样就能很方便地求出任意两点的抑或值了。
先来介绍一下位移算符“^”,相同结果是0,不同才是1。如果x^y=z,那么y^z=x且x^z=y,把整个表写出来就很清楚了。
因为gc ^ ca = ga,所有ca = ga ^ gc。同理,只要知道最近公共祖先就可以快速求得cb,查询的答案就是ca ^ cb。
在最后输出的时候,你可能会很严谨地写道:(ga ^ gc) ^ (gb ^ gc),突然发现,gc ^ gc = 0,gc没有用的!因此公共祖先都不用求了,对于每个询问,直接输出ga ^ gb即可。
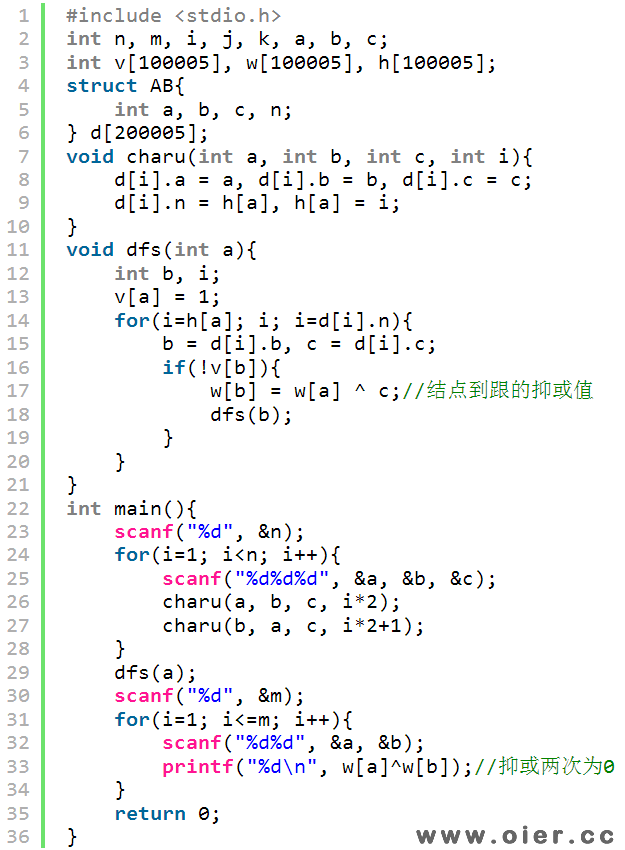
程序实现