题目大意:有n个农场,已知m个农场之间的作物多少关系,请问这些关系是否有冲突?
题目描述
小 K 在 Minecraft 里面建立很多很多的农场,总共 n 个,以至于他自己都忘记了每个农场中种植作物的具体数量了,他只记得一些含糊的信息(共 m 个),以下列三种形式描述:
- 农场 a 比农场 b 至少多种植了 c 个单位的作物。
- 农场 a 比农场 b 至多多种植了 c 个单位的作物。
- 农场 a 与农场 b 种植的作物数一样多。
但是,由于小 K 的记忆有些偏差,所以他想要知道存不存在一种情况,使得农场的种植作物数量与他记忆中的所有信息吻合。
输入输出格式
输入格式:
第一行包括两个整数 n 和 m,分别表示农场数目和小 K 记忆中的信息数目。
接下来 m 行:
如果每行的第一个数是 1,接下来有 3 个整数 a,b,c,表示农场 a 比农场 b 至少多种植了 c 个单位的作物。
如果每行的第一个数是 2,接下来有 3 个整数 a,b,c,表示农场 a 比农场 b 至多多种植了 c 个单位的作物。
如果每行的第一个数是 3,家下来有 2 个整数 a,b,表示农场 a 终止的数量和 b 一样多。
输出格式:
如果存在某种情况与小 K 的记忆吻合,输出“Yes”,否则输出“No”。
输入输出样例
输入样例#1:
3 3 3 1 2 1 1 3 1 2 2 3 2
输出样例#1:
Yes
说明
对于 100% 的数据保证:1 ≤ n,m,a,b,c ≤ 10000。
解题思路
一样多即a>=b&&b>=a;a比b至少多c即a>=b+c;a比b至多多c即a<=b+c。将所有表达式转成小于等于后求最短路,a<=b+c即b到a有一条c的边,a越小就“越满足条件”,如果有解即不会出现负环就Yes。当然,全部转成>=求最长路也是可以的,a>=b+c即b到a有一条c的边,a越大就“越满足条件”,只要没有正环就有解。
判断是否出现负环、正环,用深度比较快——搜索过程中,如果更新了搜索中的点,那么会重头再更新一圈,一直下去,因此,如果发现更新的点是访问中的就说明有环无解!
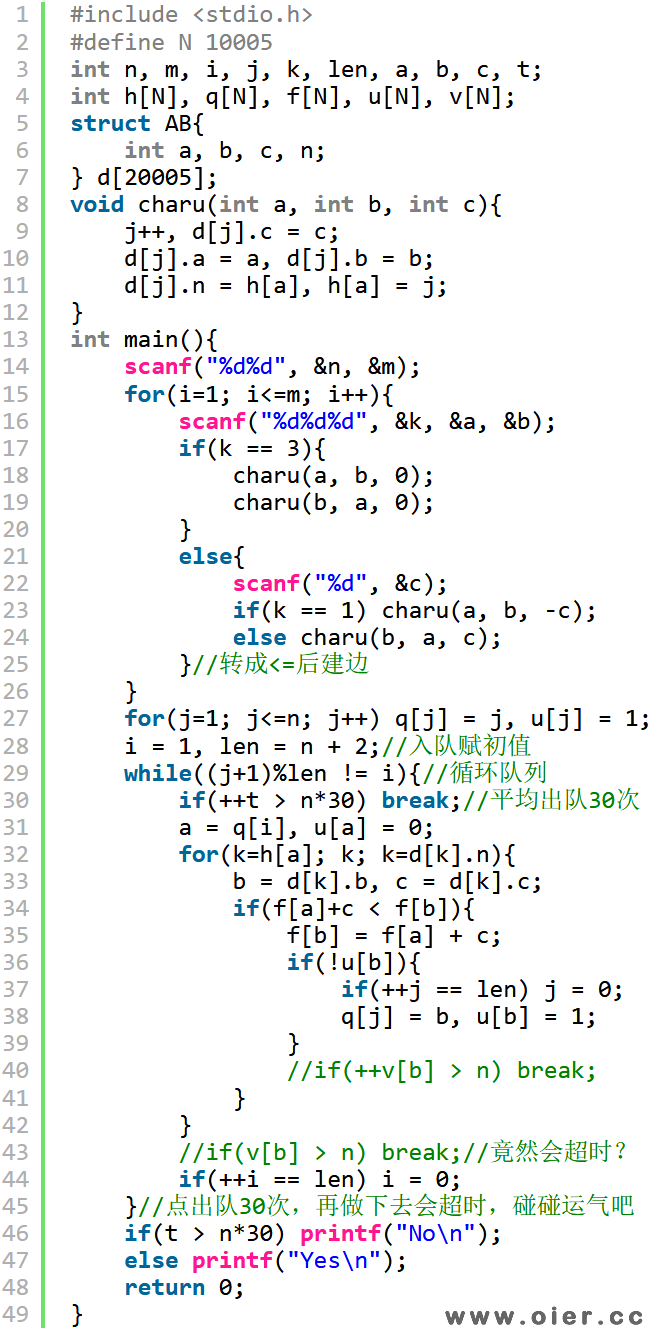
使用SPFA找环,一般是判断一个点入队超过n次就有环,但一个点入队n次,那么边也要访问n次那么多,很容易超时。SPFA一般是很快的,如果出现慢的情况,很可能就是有环,因为我们如果发现平均每个点入队很多次,超过了正常的速度,再做下去很可能超时,此时就很可能有环了。宁可答案错误,也不要超时,break输出NO吧!
为什么不能用拓扑排序?
首先可以有环,只是不允许有正环或者负环,有环就无法找到入度为0的点;如果求最长路,不能有正环,求最短路,不能有负环。假设是求最长路,那么把所有边转成正的,判断有无环不就行了吗?还是不行,因为边的含有不一样了:大于等于求最长路、小于等于求最短路。如a比b至多多1,c比b至少多1,a比c至少多1,他是无解的,但转成正边却无环。
程序实现
深搜判环,速度比SPFA快:
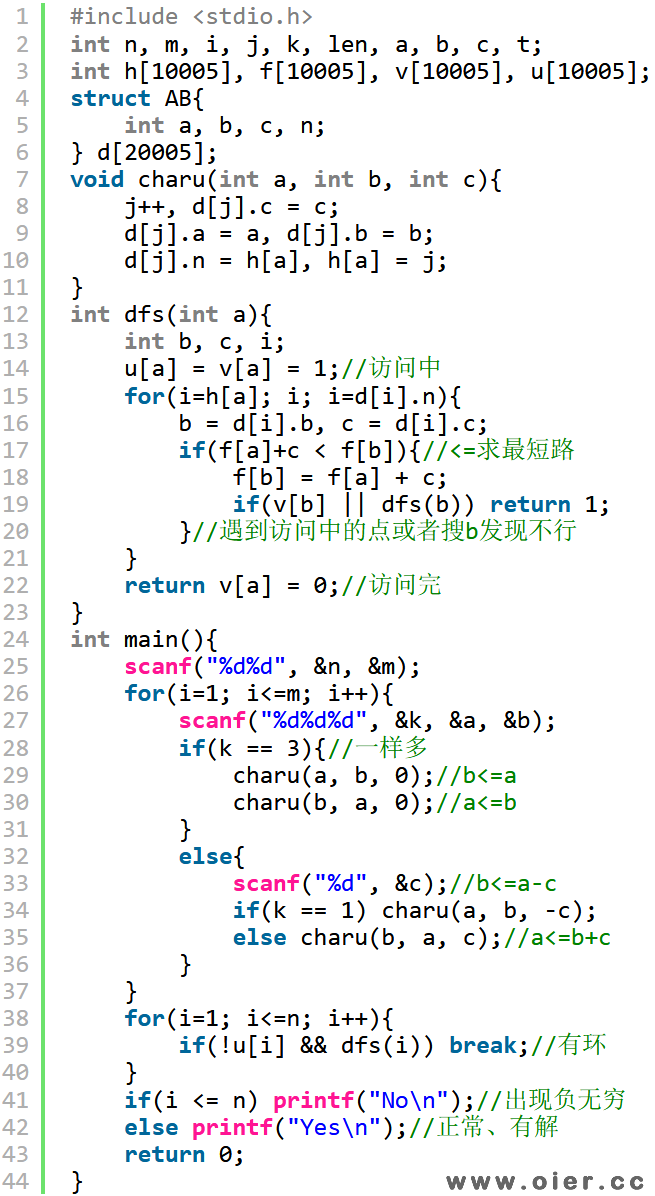
SPFA入队n次,竟然会超时。