洛谷P1958上学路线[NOI导刊]
1888+
作者:crxis 发布:2021-04-30 分类:递推
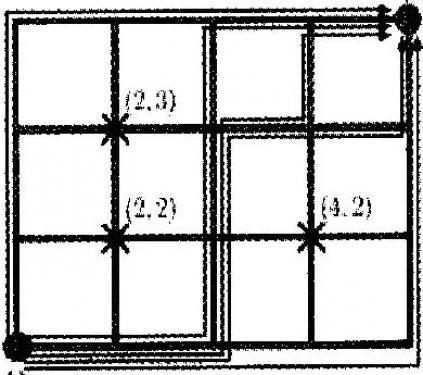
题目大意:一个棋盘,从左下角(0, 0)走到右上角(n, m)共有多少种方案?注意有些位置不能走,且每次只能往右走或者往上走。
题目描述
你所在城市的街道好像一个棋盘,有a条南北方向的街道和b条东西方向的街道。南北方向的a条街道从西到东依次编号为l到a,而东西方向的b条街道从南到北依次编号为l到b,南北方向的街道i和东西方向的街道j的交点记为(i,j)。
你住在(1,1)处,而学校在(a,b)处,你骑自行车去上学,自行车只能沿着街道走,而且为了缩短时间只允许沿着向东和北的方向行驶。
现在有N个交叉路口在施工(X1,Yl)、(X2,Y2)……,(Xn,Yn),这些路口是不能通车的。
问你上学一共有多少走法?
输入输出格式
输入格式
第一行包含两个整数a和b,并且满足1≤a,b≤16。
第二行包含一个整数N,表示有N个路口在维修(1≤N≤40)。
接下来N行,每行两个整数X\_i,Y\_i,描述路口的位置。
输出格式
输出一个整数表示从(1,1)到(a,b)的行车路线总数。
输入输出样例
输入样例 #1
5 4
3
2 2
2 3
4 2
输出样例 #1
5说明
【样例解释】
解题思路
按照坐标从小到大递推即可,遇到障碍不递推,直接设置路线为零,这样下次可以直接加它的方案数。
程序实现
